EPFL Students Projects Proposals
The projects below are available for either Bachelor/Master semester projects or Master thesis projects (the content will be adjusted accordingly). Suggestions of other projects (or variants of existing projects) are also welcome, as long as they fit within the group's research interests.
Contact: sylvain.calinonepfl.ch
Text flourishing for a robot writer: a learning and optimization approach


This project aims to generate trajectories for a robot to embellish text in an automatic manner.
Goals of the project:
An optimal control approach based on iterative linear quadratic regulator (iLQR) will be investigated for trajectory optimization. First, the problem will be approached by designing an algorithm for automatically placing a set of ellipses above and below the words to be flourished, by considering the empty spaces available based on the surrounding texts. A path optimization algorithm will then be created to generate movements by using the ellipses as guides (possibly formulated as virtual mass and gravitational forces). The objectives will be designed by transforming aesthetic guidelines for artists into a set of cost functions that can be used in optimal control.
The project will be implemented with a 6-axis UFactory Lite-6 robot (https://www.ufactory.cc/lite-6-collaborative-robot) available at Idiap.
Prerequisites: Linear algebra, programming in Python or C++
References:
Calinon, S. (2024). A Math Cookbook for Robot Manipulation.
Robotics codes from scratch (RCFS)
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch
Ergodic drawing for a robot manipulator

This project aims to generate trajectories for a drawing robot by using the principle of ergodicity.
Goals of the project:
An optimal control approach combining an iterative linear quadratic regulator (iLQR) and a cost on ergodicity will be investigated for trajectory optimization. The project will also investigate the use of electrostatic halftoning or repulsive curves as initialization process.
The project will be implemented with a 6-axis UFactory Lite-6 robot (https://www.ufactory.cc/lite-6-collaborative-robot) available at Idiap.
Prerequisites: Linear algebra, programming in Python or C++
References:
Calinon, S. (2024). A Math Cookbook for Robot Manipulation (Section 10 on ergodic control)
drozBot, the portraitist robot
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch
Deep learning for a portraitist robot application

This project aims to explore the use of generative deep learning techniques based on image diffusion for a robot portrait drawing application.
Goals of the project:
Most of the generative deep learning techniques use images as formats, but a few explored the use of vector graphics as output format, guided by text prompts for the rendering. This project will investigate the use and comparison of these techniques in the context of a robot portrait drawing application.The project will be implemented with a 6-axis UFactory Lite-6 robot (https://www.ufactory.cc/lite-6-collaborative-robot) available at Idiap.
Prerequisites: Deep learning, programming in Python or C++
References:
SVGDreamer: Text Guided SVG Generation with Diffusion Model
DiffSketcher: Text Guided Vector Sketch Synthesis through Latent Diffusion Models
VectorFusion: Text-to-SVG by Abstracting Pixel-Based Diffusion Models
SVG Differentiable Rendering: Generating vector graphics using neural networks
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch
Ergodic control for robot exploration

A conventional tracking problem in robotics is characterized by a target to reach, requiring a controller to be computed to reach this target. In ergodic control, instead of providing a single target point, a probability distribution is given to the robot, which must cover the distribution in an efficient way. Ergodic control thus consists of moving within a spatial distribution by spending time in each part of the distribution in proportion to its density (namely, ``tracking a distribution'' instead of ``tracking a point''). The resulting controller generates natural exploration behaviors, which can be exploited for active sensing, localization, surveillance, insertion tasks, etc.
In robotics, ergodic control can be exploited in a wide range of problems requiring the automatic exploration of regions of interest. This is particularly helpful when the available sensing information is not accurate enough to fulfill the task with a standard controller, but where this information can still guide the robot towards promising areas. In a collaborative task, it can also be used when the operator's input is not accurate enough to fully reproduce the task, which then requires the robot to explore around the requested input (e.g., a point of interest selected by the operator). For picking and insertion problems, ergodic control can be applied to move around the picking/insertion point, thereby facilitating the prehension/insertion. It can also be employed for active sensing and localization (either detected autonomously, or with help by the operator). Here, the robot can plan movements based on the current information density, and can recompute the commands when new measurements are available (i.e., updating the spatial distribution used as target).
Goals of the project:
Ergodic control has originally been formulated as a Spectral Multiscale Coverage (SMC) objective. Later, another ergodic control formulation has been proposed, formulated as a Heat Equation Driven Area Coverage (HEDAC) problem. This project proposes to study the pros and cons for these techniques to solve robot manipulation problems.
Prerequisites: Control theory, signal processing, programming in Python, C++ or Matlab/Octave
References:
Calinon, S. (2024). A Math Cookbook for Robot Manipulation (Section 10 on ergodic control)
Tutorial on Ergodic Control at ICRA'2024
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch
Tensor Networks for human-guided optimization in robotics
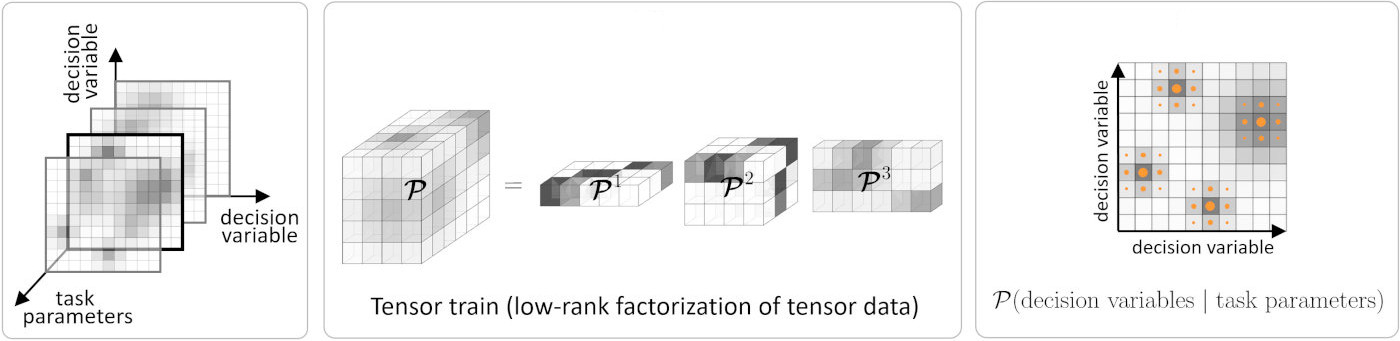
The project proposes to extend the Tensor Train for Global Optimization (TTGO) approach (see reference below) to a human-guided learning strategy. The approach will be tested with control and planning problems using robot manipulators. The formulation transforms the minimization of a cost function into the maximization of a probability density function. Hence, the problem of finding the minima of a cost function is transformed into the problem of sampling the maxima of the density function. The approach does not require gradients to be computed and can find multiple optima, which can be used for global optimization problems.
Learning and optimization problems in robotics are characterized by two types of variables: 1) task parameters representing the situation that the robot encounters, typically related to environment variables such as locations of objects, users or obstacles; and 2) decision variables related to actions that the robot takes, typically related to a controller acting within a given time window, or the use of basis functions to describe trajectories in control or state spaces. For each change of task parameters, decision variables need to be recomputed as fast as possible, so that the robot can fluently collaborate with users and can swiftly react to changes in its environment. In TTGO, the density function is modeled in the offline phase using a tensor train (TT) that learns the structure between the task parameters and the decision variables. It then allows conditional sampling over the task parameters with priority for higher-density regions. This property is used for fast online decision-making, with local Gauss-Newton optimization to refine the results, see the above figure for an overview. TTGO allows the distribution of computation into offline and online phases. It can cope with a mix of continuous and discrete variables for optimization thus providing an alternative to mixed-integer programming.
Goals of the project:
An important advantage of TTGO is that the underlying TT-cross method used to approximate the distribution in TT format can easily be extended to various forms of human-guided learning, which will be investigated in this project. The goal will be to test whether the original autonomous learning strategy of TT-Cross can be extended to a human-guided learning strategy, by letting the user sporadically specify task parameters or decision variables within the iterative process. The first case can be used to provide a scaffolding mechanism for robot skill acquisition. The second case can be used for the robot to ask for help in specific situations.
Prerequisites: Linear algebra, optimization, programming in Python or Matlab/Otave
Reference:
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch
Human body tracking with signed distance fields
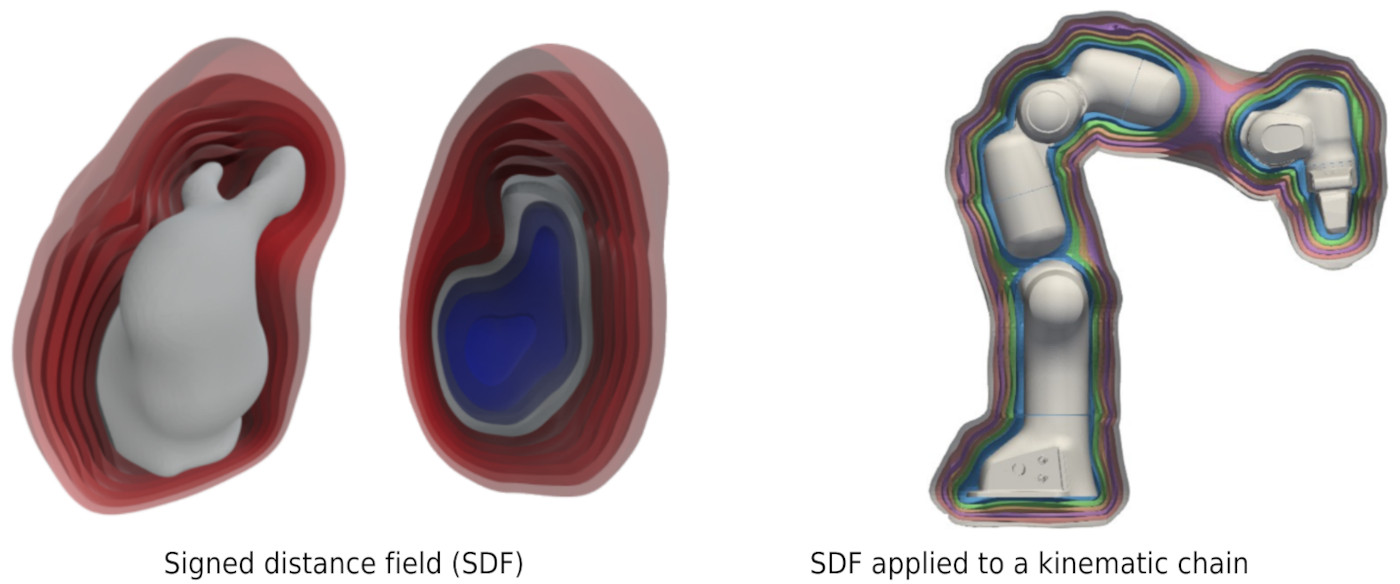
Signed distance fields (SDFs) are popular implicit shape representations in robotics. Most often, SDFs are used to represent rigid objects. However, they can also be used to represent general kinematic chains, such as articulated objects, robots, or humans. SDFs provide a continuous and differentiable representation that can easily be combined with learning, control, and optimization techniques. This project aims to explore the SDF representation of the human body based on state-of-the-art detection, tracking, and skeleton extraction techniques. The developed SDF representation can be used for human-robot interaction or transferring manipulation skills from humans to robots.
Goals of the project:
The human skeleton can be detected and tracked through images or videos using pre-trained vision models, and SDFs can be reconstructed by leveraging the SMPL-X model, a realistic 3D model for the human body based on skinning and blend shapes. This project proposes to utilize these techniques to build the SDF for the human body and then apply it to robot manipulation tasks.
Prerequisites: Machine learning, computer vision, programming in Python or C++
References:
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch, yiming.liepfl.ch (co-supervisor)
Motion generation from a geodesic distance field
Many applications require the modeling of shapes and paths as an implicit representation based on distance fields, including robotics, vision and computer graphics. Often, the derivatives of this distance function are exploited for learning, optimization, planning or control problems. The classical use case considers Euclidean distances, with the shortest path between two points corresponding to a line segment. More generally, we can define a smoothly varying weight matrix that can for example priviledge some directions over others to compute distances, which corresponds to a Riemannian metric. This is for example the case in robotics if we want to consider the effect of inertia for the generaiton of motion. In such a case, the geodesic path between two points will typically be curved. One way to compute such path is to start from one of the two points and build a potential field with an anisotropic diffusion process. After this, the path can be recovered by following the gradient of this potential field.
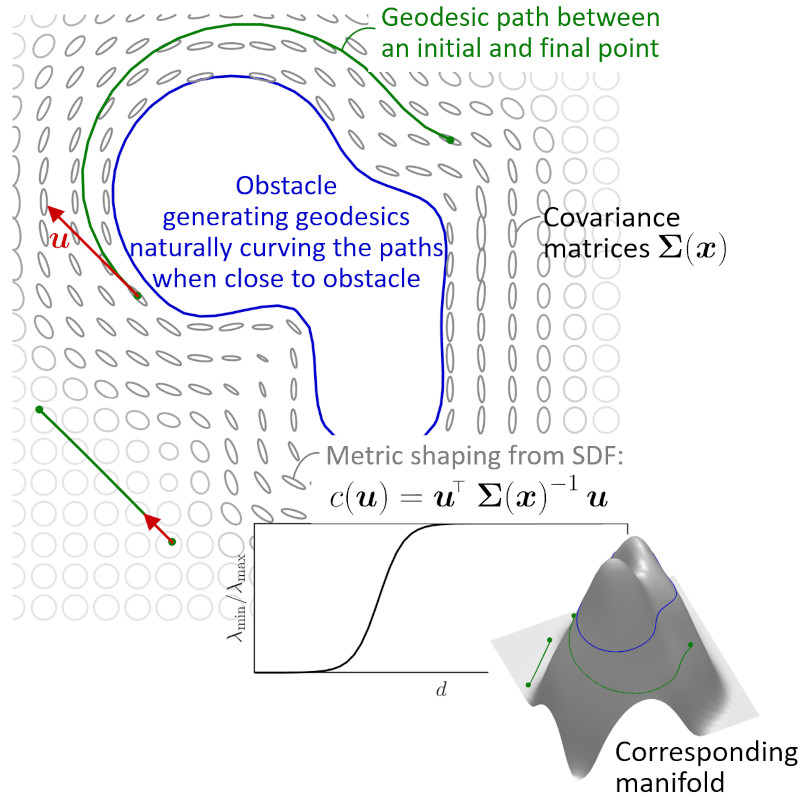
Goals of the project:
Several approaches exist to build these geodesic paths, which will be investigated in this project for the case of 3D motion to move between two pairs of points while avoiding an obstacle (blue paths on the image). The obstacle will be modeled as a distance field, with the Riemannian metric built from this distance field (ellipses on the image).
Prerequisites: Linear algebra, programming in Python or Matlab/Octave
References:
Level: Bachelor/Master (semester project or PDM)
Contact: sylvain.calinonepfl.ch