Robot Learning & Interaction
My work focuses on human-centered robotics applications in which the robots can acquire new skills from only few demonstrations and interactions. It requires the development of models that can exploit the structure and geometry of the acquired data in an efficient way, the development of optimal control techniques that can exploit the learned task variations and coordination patterns, and the development of intuitive interfaces to acquire meaningful demonstrations.
The developed approaches can be applied to a wide range of manipulation skills, with robots that are either close to us (assistive and industrial robots), parts of us (prosthetics and exoskeletons), or far away from us (teleoperation). My research is supported by the European Commission, by the Swiss National Science Foundation, by the State Secretariat for Education, Research and Innovation, and by the Swiss Innovation Agency.
You can also download my research statement as a PDF file.
LEARNING IN A HANDFUL OF TRIALS
The field of machine learning has evolved toward approaches relying on huge amounts of data. In several application domains, these big datasets are already available, or are inexpensive to collect/produce. In contrast, robotics is characterized by a different problem setting. It should instead be viewed as a wide-ranging data problem, with models that could start learning from small datasets, and that could still exploit more data if such data become available during the robot's lifespan.
The current trend of machine learning relying on big datasets can bias the development of robot learning approaches in a negative way. In contrast to other fields, the data formats in robotics vary significantly across tasks, environments, users and platforms (different sensors and actuators, not only in formats but also in modalities and organizations). Then, the learned models often need to be interpretable to provide guarantees and to be linked to other techniques. For these reasons, my work focuses on robot learning approaches that can rely on only few demonstrations or trials.
The main challenge boils down to finding structures that can be used in a wide range of tasks, which are discussed next and include (from high level to low level):
Efficient robot skills acquisition requires the right trade-off between learning and exploitation of these different form of structures (at model and algorithm levels).
GEOMETRIC STRUCTURES
Because robots act in a physical world, many fundamental problems in robotics involve geometry, leading to an increased research effort in geometric methods for robotics in the recent years. To speed up skills acquisition, the prior knowledge about the physical world can be embedded within the representations of skills and associated learning algorithms. Our work focuses on Riemannian geometry and geometric algebra to provide such structures.
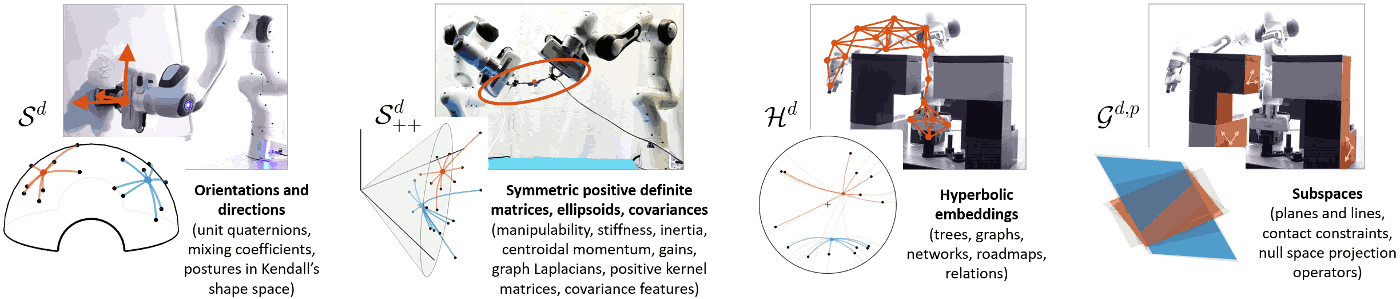
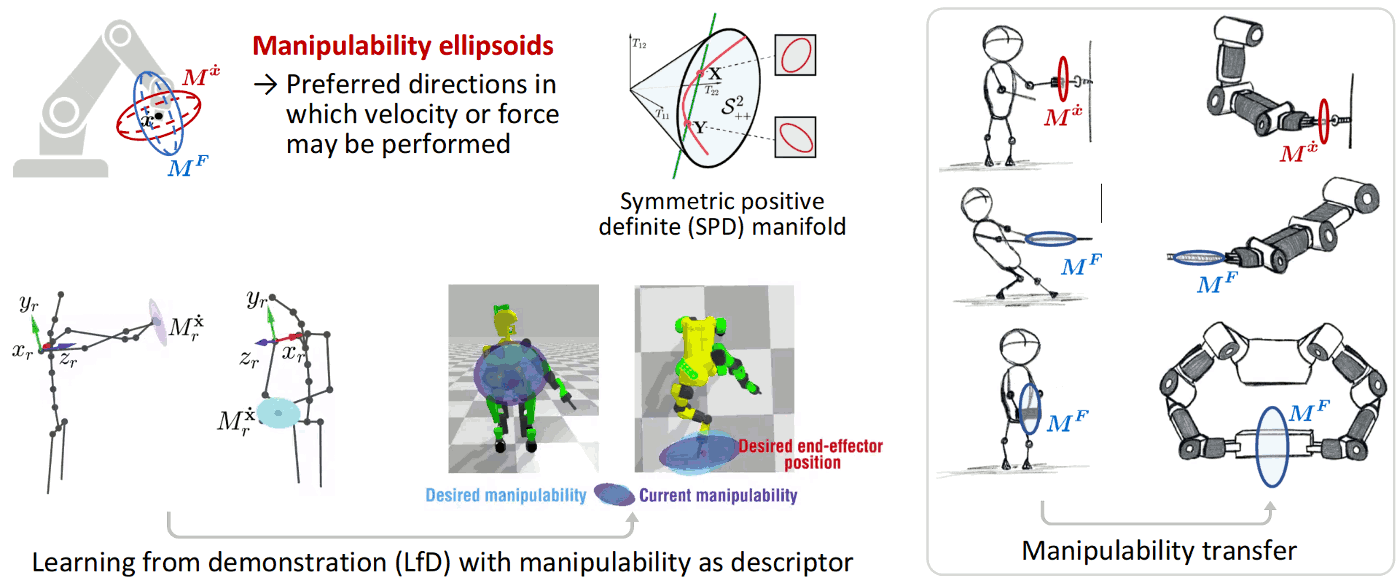
Skills transfer can exploit stiffness and manipulability ellipsoids, in the form of geometric descriptors representing the skills to be transferred to the robot. As these ellipsoids lie on symmetric positive definite (SPD) manifolds, Riemannian geometry can be used to learn and reproduce these descriptors in a probabilistic manner.
Reference:
Jaquier, N., Rozo, L. and Calinon, S. (2020). Analysis and Transfer of Human Movement Manipulability in Industry-like Activities. In Proc. of IEEE/RSJ Intl Conf. on Intelligent Robots and Systems (IROS), pp. 11131-11138. info pdf
Another promising candidate for handling geometric structures in robotics is the framework of geometric algebra, whose roots can be found in Clifford algebra, a unification of quaternions and Grassmann algebra. Geometric algebra can be seen as a unification of various frameworks popular in robotics, such as screw theory, Lie algebra or dual quaternions, while offering great generalization and extension perspectives.
In standard linear algebra, a point in a 3D space can be reached by taking different linear combinations of three basis vectors $\bm{e}_1$, $\bm{e}_2$, and $\bm{e}_3$, where all linear combinations of the basis vectors form individual subspaces of the 3D space. In geometric algebra, more elaborated subspaces are considered, including higher order elements such as bivectors, which are subspaces spanned by the outer product of two one-dimensional subspaces (e.g., $\bm{e}_1 \wedge \bm{e}_2$). The cross product in linear algebra is a special case of the outer product, which is valid only for 3D vectors, and whose result is given in the form of a vector. In contrast, the outer product can be applied to any dimensions, whose result represents an oriented space (e.g., area, volume) swept by the vectors. Geometric algebra relies on the notion of a geometric product, which is the sum of an inner and outer product $\bm{e}_1 \bm{e}_2 = \bm{e}_1 \cdot \bm{e}_2 + \bm{e}_1 \wedge \bm{e}_2$. The resulting elements are called multivectors. This representation allows geometric primitives to be encoded in a uniform manner, by representing 3D geometric objects in a higher dimension space. Both geometric objects and transformations use the same algebra and can then also be represented in a homogeneous manner as elements of this higher dimension space.
This representation is thus an interesting candidate to provide a single algebra for geometric reasoning, alleviating the need of utilizing multiple algebras to express geometric relations. While previous solutions typically needed to mix different formalisms, our work explores how the unification of concepts provided by geometric algebra can be used to solve diverse manipulation problems without leaving the proposed algebra. In robotics, geometric algebra operations typically allow translations and rotations to be treated in the same way, without requiring us to switch between different algebras, as is classically done when handling position data in a Cartesian space and orientation data as quaternions. Practically, geometric algebra allows geometric operations to be computed in a very fast way, with compact codes.
Our work leverages the capabilities of geometric algebra in robot manipulation tasks. We show in [Löw and Calinon, 2022] below that the modeling of cost functions for optimal control can be done uniformly across different geometric primitives, leading to a low symbolic complexity of the resulting expressions and a geometric intuitiveness. Our benchmarks also show that such an approach provides faster resolution of robot kinematics problems than state-of-the-art software libraries used in robotics.
References:
Calinon, S. (2020). Gaussians on Riemannian Manifolds: Applications for Robot Learning and Adaptive Control. IEEE Robotics and Automation Magazine (RAM), 27:2, 33-45. info pdf
Jaquier, N., Rozo, L., Caldwell, D.G. and Calinon, S. (2021). Geometry-aware Manipulability Learning, Tracking and Transfer. International Journal of Robotics Research (IJRR), 40:2-3, 624-650. info pdf
Löw, T. and Calinon, S. (2023). Geometric Algebra for Optimal Control with Applications in Manipulation Tasks. IEEE Trans. on Robotics (T-RO), 39:5, 3586-3600. info pdf
DATA STRUCTURES
Another type of structure that we exploit relates to the organization of data as multidimensional arrays (also called tensors). These data appear in various robotic tasks, either as the natural organization of sensory/motor data (tactile arrays, images, kinematic chains), as the result of standardized preprocessing steps (moving time windows, covariance features), data in multiple coordinate systems, or in the form of basis functions decompositions. Developed in the fields of multilinear algebra and tensor methods, these approaches extend linear factorization techniques such as singular value decomposition to multilinear decomposition, without requiring the transformation of the tensors to vectors or matrices. We exploit these techniques to provide robots with the capability to learn tasks from only few tensor datapoints, by relying on the multidimensional nature of the data.
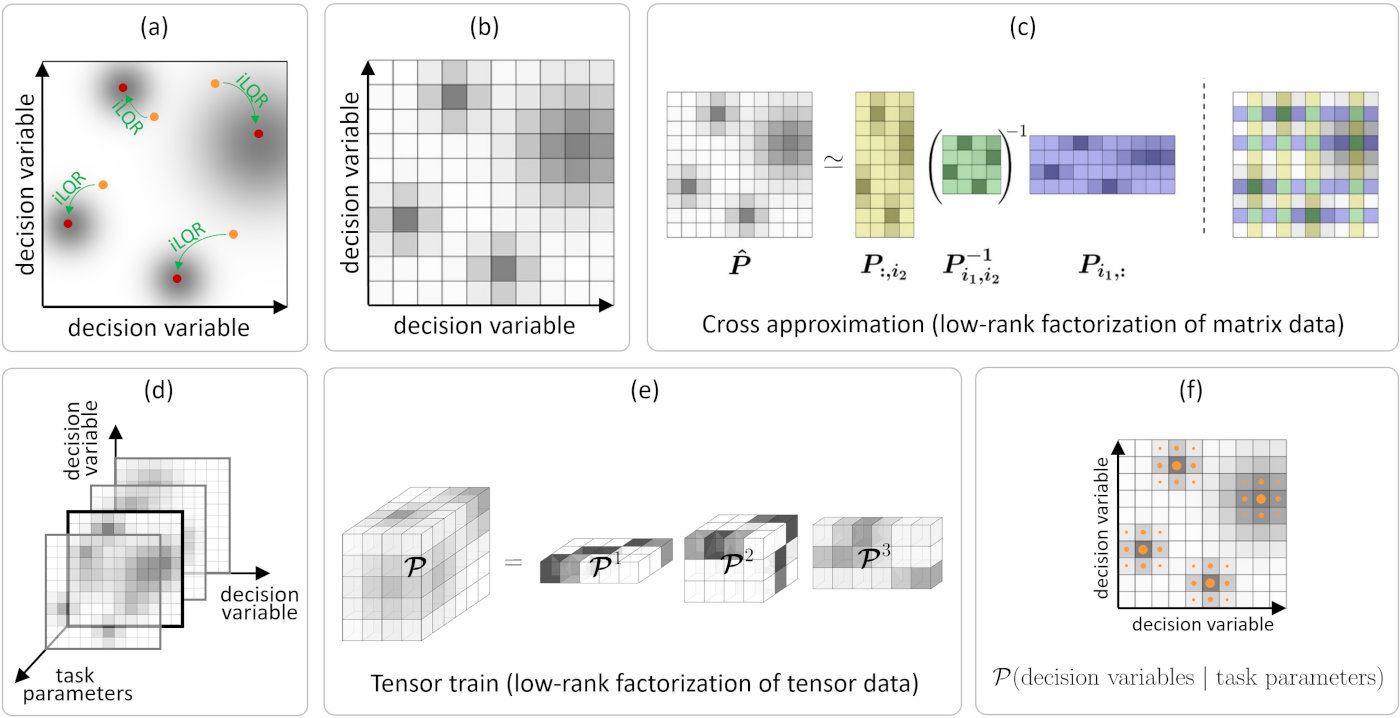
Learning and optimization problems in robotics are characterized by two types of variables: 1) task parameters representing the situation that the robot encounters, typically related to environment variables such as locations of objects, users or obstacles; and 2) decision variables related to actions that the robot takes, typically related to a controller acting within a given time window, or the use of basis functions to describe trajectories in control or state spaces. For each change of task parameters, decision variables need to be recomputed as fast as possible, so that the robot can fluently collaborate with users and can swiftly react to changes in its environment.
Within the MEMMO and LEARN-REAL projects, we investigate the roles of offline and online learning for optimal control. The problem is formalized as an optimization problem with a cost function to minimize, parameterized by task parameters and decision variables. The formulation transforms the minimization of a cost function into the maximization of a corresponding probability density function. Hence, the problem of finding the minima of a cost function is transformed into the problem of sampling the maxima of the density function. The proposed approach does not require gradients to be computed and can find multiple optima, which can be used for global optimization problems.
The density function is modeled in the offline phase using a tensor train (TT) that exploits the structure between the task parameters and the decision variables. Tensor train factorization is a modern tool for the representation of complex nonlinear functions in variable separation form, with robust techniques such as TT-Cross to find the representation. It allows conditional sampling over the task parameters with priority for higher-density regions. This property is used for fast online decision-making, with local Gauss-Newton optimization to refine the results, see the above Figure for an overview.
The proposed tensor train for global optimization (TTGO) approach has several advantages for robot skills acquisition. First, the problem formulation makes it a ubiquitous tool. It allows the distribution of computation into offline and online phases. It can cope with a mix of continuous and discrete variables for optimization thus providing an alternative to mixed-integer programming. By construction, the decision variables also stay within a bounded domain, which can be advantageous in some problems (e.g., joint angle limits, control bounds). Another important advantage of TTGO is that the underlying TT-cross method used to approximate the distribution in TT format can easily be extended to various forms of human-guided learning, by letting the user sporadically specify task parameters or decision variables within the iterative process. The first case can be used to provide a scaffolding mechanism for robot skill acquisition. The second case can be used for the robot to ask for help in specific situations.
In the reference below, we demonstrated the capability of the approach for trajectory optimization within a varied set of control and planning problems with robot manipulators.
In robotics, ergodic control extends the tracking principle by specifying a probability distribution over an area to cover instead of a trajectory to track. The original problem is formulated as a spectral multiscale coverage problem, typically requiring the spatial distribution to be decomposed as Fourier series. This approach does not scale well to control problems requiring exploration in search space of more than 2 dimensions. To address this issue, we propose the use of tensor trains, a recent low-rank tensor decomposition technique from the field of multilinear algebra. The proposed solution is efficient, both computationally and storage-wise, hence making it suitable for its online implementation in robotic systems. The approach is applied to a peg-in-hole insertion task requiring full 6D end-effector poses (see second reference below).
References:
Shetty, S., Lembono, T., Löw, T. and Calinon, S. (2023). Tensor Train for Global Optimization Problems in Robotics. International Journal of Robotics Research (IJRR). info pdf
Shetty, S., Silvério, J. and Calinon, S. (2022). Ergodic Exploration using Tensor Train: Applications in Insertion Tasks. IEEE Trans. on Robotics (T-RO), 38:2, 906-921. info pdf
COMBINATION STRUCTURES
Movement primitives are often used in robot learning as high-level "bricks" of motion from a dictionary that can be re-organized in series and in parallel. Our work extends this notion to behavior primitives, which form a richer set of behaviors (see (a) in the figure below). These behavior primitives correspond to controllers that are either myopic or anticipative, with either time-independent or time-dependent formulations.
We propose to formalize the combination of behavior primitives as an information fusion problem in which several sources of information can be modeled as probability distributions. The product of experts (PoE) is a machine learning technique modeling a probability distribution by combining the output from several simpler distributions. The core idea is to combine several distributions (called experts) by multiplying their density functions. This allows each expert to make decisions on the basis of a few dimensions, without having to cover the full dimensionality of a problem. A PoE corresponds to an "and" operation, which contrasts with a mixture model that corresponds to an "or" operation (by combining several probability distributions as a weighted sum of their density functions). Thus, each component in a PoE represents a soft constraint. For an event to be likely under a product model, all constraints must be (approximately) satisfied. In contrast, in a mixture model, an event is likely if it matches (approximately) with any single expert.
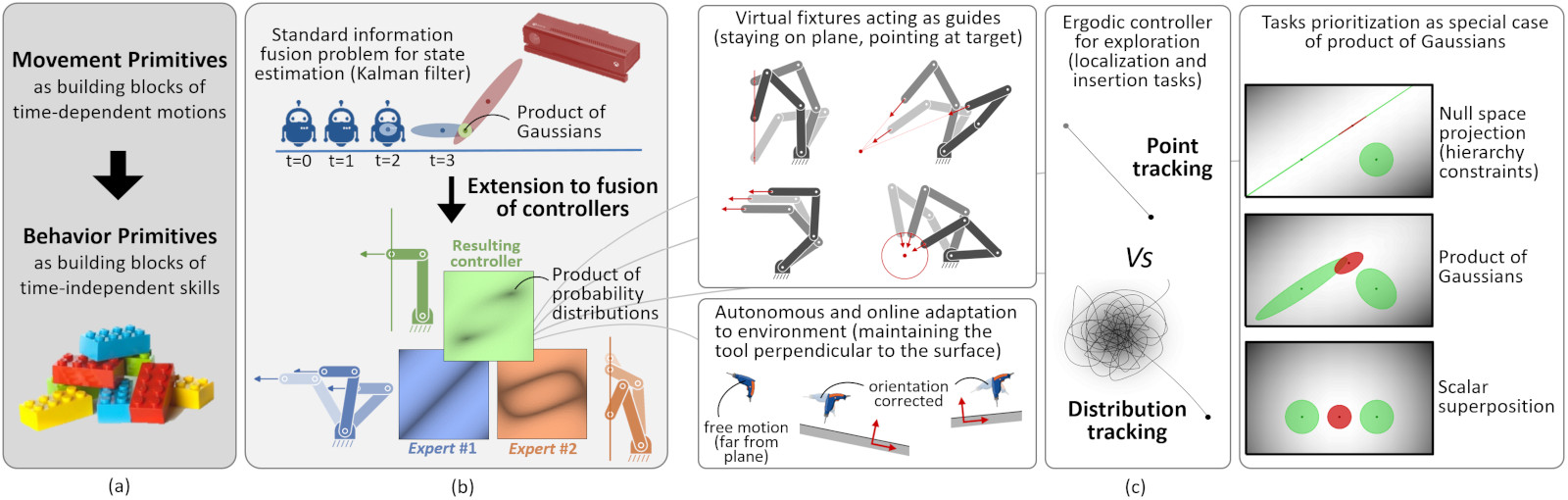
With Gaussian distributions, the fusion problem simplifies to a product of Gaussians (PoG), which can be solved analytically, where the distributions can either represent robot commands at the current time step (myopic control system), or trajectory distributions in the control space (anticipative planning system).
State estimation is also classically solved as an information fusion problem, resulting in a product of Gaussians that takes into account uncertainty in motion and sensor(s) models (a well-known example is the Kalman filter), see (b) in the figure above. We propose to treat the combination of behavior primitives within a similar mathematical framework, by relying on products of experts, where each expert takes care of a specific aspect of the task to achieve.
This approach allows the orchestration of different controllers, which can be learned separately or altogether (by variational inference). With this formulation, the robot can counteract perturbations that have an impact on the fulfillment of the task, while ignoring other perturbations. It also allows us to create bridges with research in biomechanics and motor control, with formulations including minimal intervention principles, uncontrolled manifolds or optimal feedback control.
To facilitate the acquisition of manipulation skills, task-parameterized models can be exploited to take into account that motions typically relates to objects, tools or landmarks in the robot's workspace. The approach consists of encoding a movement in multiple coordinate systems (e.g., from the perspectives of different objects), in the form of trajectory distributions. In a new situation (e.g., for new object locations), the reproduction problem corresponds to a fusion problem, where the variations in the different coordinate systems are exploited to generate a movement reference tracked with variable gains, providing the robot with a variable impedance behavior that automatically adapts to the precision required in the different phases of the task. For example, in a pick-and-place task, the robot will be stiff if the object needs to be reached/dropped in a precise way, and will remain compliant in the other parts of the task.
Our ongoing work explores the extension of the task-parameterized principle to a richer set of behaviors, including coordinate systems that take into account symmetries (e.g., cylindrical and spherical coordinate systems) and nullspace projection structures.
References:
Calinon, S. (2016). A Tutorial on Task-Parameterized Movement Learning and Retrieval. Intelligent Service Robotics (Springer), 9:1, 1-29. info pdf
Silvério, J., Calinon, S., Rozo, L. and Caldwell, D.G. (2019). Learning Task Priorities from Demonstrations. IEEE Transactions on Robotics, 35:1, 78-94. info pdf
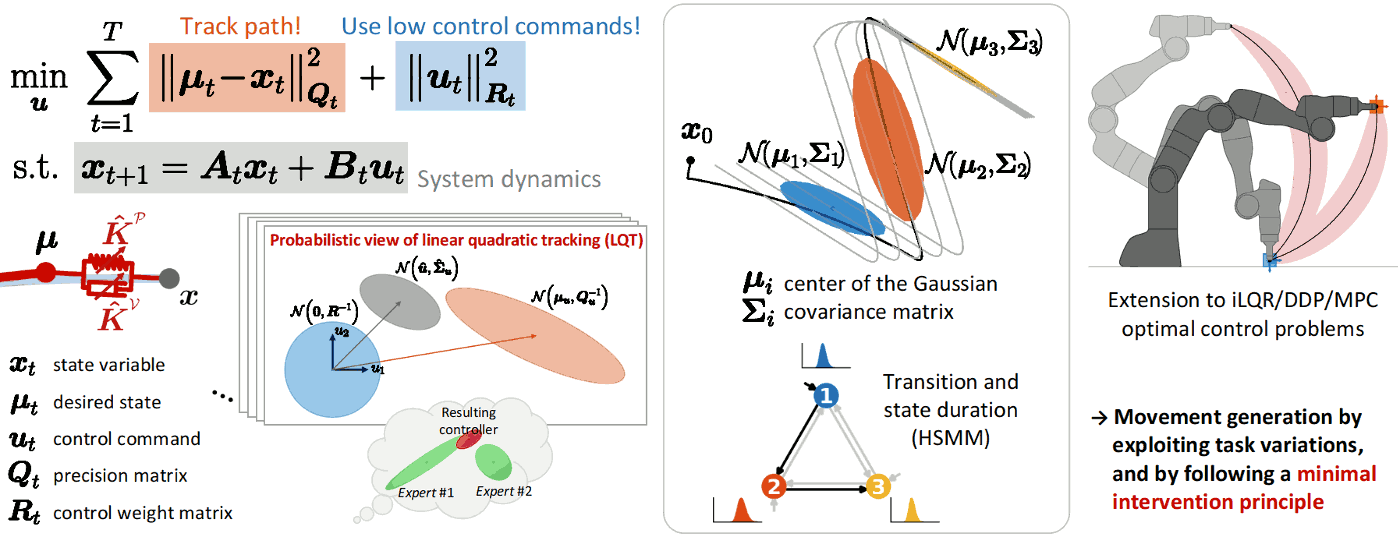
Linear quadratic tracking (LQT) is a simple form of optimal control that trades off tracking and control costs expressed as quadratic terms over a time horizon, with the evolution of the state described in a linear form. This constrained problem can be solved by expressing the state and the control commands as trajectories, corresponding to a least squares solution. A probabilistic interpretation of the LQT solution can be built by using the residuals of this estimate.
This approach allows the creation of bridges between learning and control. For example, in learning from demonstration, the observed (co)variations in a task can be formulated as an LQT objective function, which then provides a trajectory distribution in control space that can be converted to a trajectory distribution in state space. All the operations are analytic and only exploit basic linear algebra.
The proposed approach can also be extended to model predictive control (MPC), iterative LQR (iLQR) and differential dynamic programming (DDP), whose solution needs this time to be interpreted locally at each iteration step of the algorithm.
References:
Calinon, S. and Lee, D. (2019). Learning Control. Vadakkepat, P. and Goswami, A. (eds.). Humanoid Robotics: a Reference, pp. 1261-1312. Springer. info pdf
Calinon, S. (2016). Stochastic learning and control in multiple coordinate systems. Intl Workshop on Human-Friendly Robotics (HFR). info pdf
LEARNING STRUCTURES
To reduce the amount of required data, another opportunity to seize is that machine learning in robotics goes beyond the standard training-set and testing-set paradigm.
Indeed, we can exploit a number of interactive learning mechanisms to acquire/generate better data on-the-spot, including active learning, machine teaching (by generating data to train our robots), curriculum learning (by providing data of increased complexity that adapt to the learner), and bilateral interactions that rely on several social mechanisms to transfer skills more efficiently. Thus, skills acquisition in robotics is a scaffolding process rather than a standard learning process. In this scaffolding metaphor, the robot first needs a lot of structures, and the structures can be progressively dismantled when the robot progresses. There is thus a continuous evolution from full assistance to full autonomy.
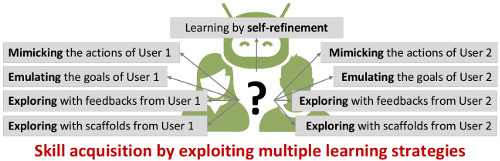
We can also greatly benefit from the orchestration of several learning modalities that can jointly be used to transfer skills, and evaluate the current capability of the robot to execute the task. This can improve the robustness of skill acquisition by allowing diverse forms of environment and user constraints to be considered, and an improved assessment of the robot knowledge (by testing the acquired knowledge in diverse situations).
The other important advantage is that this orchestration allows each individual learning modality to be simplified, as skills acquisition with a single learning strategy can be unnecessarily complex. Indeed, we could not learn to play a sport efficiently without practice, by only observing others play. We could also not acquire efficiently a fabrication skill with only the desired end-goal. We instead need to observe an expert or to to be guided throughout the process to acquire the underlying fabrication strategies. Similarly to us, robots cannot acquire skills efficiently by using a single learning modality.
Thus, instead of focusing on the improvement of algorithms and models for a specific learning strategy, I believe that robotics could highly benefit from the meta-learning problem of combining learning modalities, without defining the sequence and organization in advance.