Python API

This section includes information for using the pure Python API of bob::measure.

bob.measure.mse(estimation, target)

Calculates the mean square error between a set of outputs and target values using the following formula:

Estimation (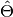) and target (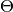) are supposed to have 2 dimensions. Different examples are organized as rows while different features in the estimated values or targets are organized as different columns.

bob.measure.rmse(estimation, target)

Calculates the root mean square error between a set of outputs and target values using the following formula:

Estimation (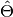) and target (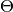) are supposed to have 2 dimensions. Different examples are organized as rows while different features in the estimated values or targets are organized as different columns.

bob.measure.relevance(input, machine)

Calculates the relevance of every input feature to the estimation process using the following definition from:

Neural Triggering System Operating on High Resolution Calorimetry Information, Anjos et al, April 2006, Nuclear Instruments and Methods in Physics Research, volume 559, pages 134-138

In other words, the relevance of a certain input feature i is the change on the machine output value when such feature is replaced by its mean for all input vectors. For this to work, the input parameter has to be a 2D array with features arranged column-wise while different examples are arranged row-wise.

bob.measure.recognition_rate(cmc_scores)

Calculates the recognition rate from the given input, which is identical to the rank 1 (C)MC value.

The input has a specific format, which is a list of two-element tuples. Each of the tuples contains the negative and the positive scores for one test item. To read the lists from score files in 4 or 5 column format, please use the bob.measure.load.cmc_four_column() or bob.measure.load.cmc_five_column() function.

The recognition rate is defined as the number of test items, for which the positive score is greater than or equal to all negative scores, divided by the number of all test items. If several positive scores for one test item exist, the highest score is taken.

bob.measure.cmc(cmc_scores)

Calculates the cumulative match characteristic (CMC) from the given input.

The input has a specific format, which is a list of two-element tuples. Each of the tuples contains the negative and the positive scores for one test item. To read the lists from score files in 4 or 5 column format, please use the bob.measure.load.cmc_four_column() or bob.measure.load.cmc_five_column() function.

For each test item the probability that the rank r of the positive score is calculated. The rank is computed as the number of negative scores that are higher than the positive score. If several positive scores for one test item exist, the highest positive score is taken. The CMC finally computes how many test items have rank r or higher.

bob.measure.get_config()

Returns a string containing the configuration information.

bob.measure.correctly_classified_negatives(negatives, threshold) → int

This method returns an array composed of booleans that pin-point which negatives where correctly classified in a “negative” score sample, given a threshold. It runs the formula: foreach (element k in negative) if negative[k] < threshold: returnValue[k] = true else: returnValue[k] = false

bob.measure.correctly_classified_positives(positives, threshold) → numpy.ndarray

This method returns a 1D array composed of booleans that pin-point which positives where correctly classified in a ‘positive’ score sample, given a threshold. It runs the formula: foreach (element k in positive) if positive[k] >= threshold: returnValue[k] = true else: returnValue[k] = false

bob.measure.det(negatives, positives, n_points) → numpy.ndarray

Calculates points of an Detection Error-Tradeoff Curve (DET).

Calculates the DET curve given a set of positive and negative scores and a desired number of points. Returns a two-dimensional array of doubles that express on its rows:

[0]

X axis values in the normal deviate scale for the false-rejections

[1]

Y axis values in the normal deviate scale for the false-accepts

You can plot the results using your preferred tool to first create a plot using rows 0 and 1 from the returned value and then replace the X/Y axis annotation using a pre-determined set of tickmarks as recommended by NIST. The algorithm that calculates the deviate scale is based on function ppndf() from the NIST package DETware version 2.1, freely available on the internet. Please consult it for more details. By 20.04.2011, you could find such package here.

bob.measure.eer_rocch(negatives, positives) → float

Calculates the equal-error-rate (EER) given the input data, on the ROC Convex Hull as done in the Bosaris toolkit (https://sites.google.com/site/bosaristoolkit/).

bob.measure.eer_threshold(negatives, positives) → float

Calculates the threshold that is as close as possible to the equal-error-rate (EER) given the input data. The EER should be the point where the FAR equals the FRR. Graphically, this would be equivalent to the intersection between the ROC (or DET) curves and the identity.

bob.measure.epc(dev_negatives, dev_positives, test_negatives, test_positives, n_points) → numpy.ndarray

Calculates points of an Expected Performance Curve (EPC).

Calculates the EPC curve given a set of positive and negative scores and a desired number of points. Returns a two-dimensional blitz::Array of doubles that express the X (cost) and Y (HTER on the test set given the min. HTER threshold on the development set) coordinates in this order. Please note that, in order to calculate the EPC curve, one needs two sets of data comprising a development set and a test set. The minimum weighted error is calculated on the development set and then applied to the test set to evaluate the half-total error rate at that position.

The EPC curve plots the HTER on the test set for various values of ‘cost’. For each value of ‘cost’, a threshold is found that provides the minimum weighted error (see bob.measure.min_weighted_error_rate_threshold()) on the development set. Each threshold is consecutively applied to the test set and the resulting HTER values are plotted in the EPC.

The cost points in which the EPC curve are calculated are distributed uniformily in the range .

bob.measure.f_score(negatives, positives, threshold[, weight=1.0]) → float

This method computes F-score of the accuracy of the classification. It is a weighted mean of precision and recall measurements. The weight parameter needs to be non-negative real value. In case the weight parameter is 1, the F-score is called F1 score and is a harmonic mean between precision and recall values.

bob.measure.far_threshold(negatives, positives[, far_value=0.001]) → float

Computes the threshold such that the real FAR is at least the requested far_value.

Keyword parameters:

negatives

The impostor scores to be used for computing the FAR

positives

The client scores; ignored by this function

far_value

The FAR value where the threshold should be computed

Returns the computed threshold (float)

bob.measure.farfrr(negatives, positives, threshold) -> (float, float)

Calculates the false-acceptance (FA) ratio and the FR false-rejection (FR) ratio given positive and negative scores and a threshold. positives holds the score information for samples that are labelled to belong to a certain class (a.k.a., ‘signal’ or ‘client’). negatives holds the score information for samples that are labelled not to belong to the class (a.k.a., ‘noise’ or ‘impostor’).

It is expected that ‘positive’ scores are, at least by design, greater than negative scores. So, every positive value that falls bellow the threshold is considered a false-rejection (FR). negative samples that fall above the threshold are considered a false-accept (FA).

Positives that fall on the threshold (exactly) are considered correctly classified. Negatives that fall on the threshold (exactly) are considered incorrectly classified. This equivalent to setting the comparision like this pseudo-code:

foreach (positive as K) if K < threshold: falseRejectionCount += 1 foreach (negative as K) if K >= threshold: falseAcceptCount += 1

The threshold value does not necessarily have to fall in the range covered by the input scores (negatives and positives altogether), but if it does not, the output will be either (1.0, 0.0) or (0.0, 1.0) depending on the side the threshold falls.

The output is in form of a tuple of two double-precision real numbers. The numbers range from 0 to 1. The first element of the pair is the false-accept ratio. The second element of the pair is the false-rejection ratio.

It is possible that scores are inverted in the negative/positive sense. In some setups the designer may have setup the system so positive samples have a smaller score than the negative ones. In this case, make sure you normalize the scores so positive samples have greater scores before feeding them into this method.

bob.measure.frr_threshold(negatives, positives[, frr_value=0.001]) → float

Computes the threshold such that the real FRR is at least the requested frr_value.

Keyword parameters:

negatives

The impostor scores; ignored by this function

positives

The client scores to be used for computing the FRR

frr_value

The FRR value where the threshold should be computed

Returns the computed threshold (float)

bob.measure.min_hter_threshold(negatives, positives) → float

Calculates the min_weighted_error_rate_threshold() with the cost set to 0.5.

bob.measure.min_weighted_error_rate_threshold(negatives, positives, cost) → float

Calculates the threshold that minimizes the error rate, given the input data. An optional parameter ‘cost’ determines the relative importance between false-accepts and false-rejections. This number should be between 0 and 1 and will be clipped to those extremes. The value to minimize becomes: ER_cost = [cost * FAR] + [(1-cost) * FRR]. The higher the cost, the higher the importance given to not making mistakes classifying negatives/noise/impostors.

bob.measure.ppndf(value) → float

Returns the Deviate Scale equivalent of a false rejection/acceptance ratio.

The algorithm that calculates the deviate scale is based on function ppndf() from the NIST package DETware version 2.1, freely available on the internet. Please consult it for more details.

bob.measure.precision_recall(negatives, positives, threshold) -> (float, float)

Calculates the precision and recall (sensitiveness) values given positive and negative scores and a threshold. positives holds the score information for samples that are labeled to belong to a certain class (a.k.a., ‘signal’ or ‘client’). negatives holds the score information for samples that are labeled not to belong to the class (a.k.a., ‘noise’ or ‘impostor’). For more precise details about how the method considers error rates, please refer to the documentation of the method farfrr().

bob.measure.precision_recall_curve(negatives, positives, n_points) → numpy.ndarray

Calculates the precision-recall curve given a set of positive and negative scores and a number of desired points. Returns a two-dimensional array of doubles that express the X (precision) and Y (recall) coordinates in this order. The points in which the curve is calculated are distributed uniformly in the range [min(negatives, positives), max(negatives, positives)].

bob.measure.roc(negatives, positives, n_points) → numpy.ndarray

Calculates points of an Receiver Operating Characteristic (ROC).

Calculates the ROC curve given a set of positive and negative scores and a desired number of points. Returns a two-dimensional array of doubles that express the X (FRR) and Y (FAR) coordinates in this order. The points in which the ROC curve are calculated are distributed uniformily in the range [min(negatives, positives), max(negatives, positives)].

bob.measure.roc_for_far(negatives, positives, far_list) → numpy.ndarray

Calculates the ROC curve given a set of positive and negative scores and the FAR values for which the CAR should be computed. The resulting ROC curve holds a copy of the given FAR values (row 0), and the corresponding FRR values (row 1).

bob.measure.rocch(negatives, positives) → numpy.ndarray

Calculates the ROC Convex Hull curve given a set of positive and negative scores. Returns a two-dimensional array of doubles that express the X (FRR) and Y (FAR) coordinates in this order.

bob.measure.rocch2eer(pmiss_pfa) → float

Calculates the threshold that is as close as possible to the equal-error-rate (EER) given the input data.