User Guide¶

Methods in the bob.measure module can help you to quickly and easily evaluate error for multi-class or binary classification problems. If you are not yet familiarized with aspects of performance evaluation, we recommend the following papers for an overview of some of the methods implemented.

Bengio, S., Keller, M., Mariéthoz, J. (2004). The Expected Performance Curve. International Conference on Machine Learning ICML Workshop on ROC Analysis in Machine Learning, 136(1), 1963–1966.
Martin, A., Doddington, G., Kamm, T., Ordowski, M., & Przybocki, M. (1997). The DET curve in assessment of detection task performance. Fifth European Conference on Speech Communication and Technology (pp. 1895-1898).

Overview¶

A classifier is subject to two types of errors, either the real access/signal is rejected (false rejection) or an impostor attack/a false access is accepted (false acceptance). A possible way to measure the detection performance is to use the Half Total Error Rate (HTER), which combines the False Rejection Rate (FRR) and the False Acceptance Rate (FAR) and is defined in the following formula:

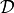$HTER(\tau, \mathcal{D}) = \frac{FAR(\tau, \mathcal{D}) + FRR(\tau, \mathcal{D})}{2} \quad \textrm{[\%]}$

where $\mathcal{D}$ denotes the dataset used. Since both the FAR and the FRR depends on the threshold 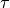$\tau$ , they are strongly related to each other: increasing the FAR will reduce the FRR and vice-versa. For this reason, results are often presented using either a Receiver Operating Characteristic (ROC) or a Detection-Error Tradeoff (DET) plot, these two plots basically present the FAR versus the FRR for different values of the threshold. Another widely used measure to summarise the performance of a system is the Equal Error Rate (EER), defined as the point along the ROC or DET curve where the FAR equals the FRR.

However, it was noted in by Bengio et al. (2004) that ROC and DET curves may be misleading when comparing systems. Hence, the so-called Expected Performance Curve (EPC) was proposed and consists of an unbiased estimate of the reachable performance of a system at various operating points. Indeed, in real-world scenarios, the threshold 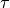$\tau$ has to be set a priori: this is typically done using a development set (also called cross-validation set). Nevertheless, the optimal threshold can be different depending on the relative importance given to the FAR and the FRR. Hence, in the EPC framework, the cost $\beta \in [0;1]$ is defined as the tradeoff between the FAR and FRR. 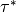The optimal threshold $\tau^*$ is then computed using different values of 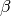$\beta$ , corresponding to different operating points:

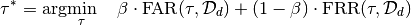
$\tau^{*} = \arg\!\min_{\tau} \quad \beta \cdot \textrm{FAR}(\tau, \mathcal{D}_{d}) + (1-\beta) \cdot \textrm{FRR}(\tau, \mathcal{D}_{d})$

where 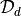$\mathcal{D}_{d}$ denotes the development set and should be completely separate to the evaluation set mathcal{D}.

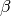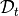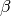Performance for different values of $\beta$ is then computed on the test set $\mathcal{D}_{t}$ using the previously derived threshold. Note that setting $\beta$ to 0.5 yields to the Half Total Error Rate (HTER) as defined in the first equation.

Note

Most of the methods availabe in this module require as input a set of 2 numpy.ndarray objects that contain the scores obtained by the classification system to be evaluated, without specific order. Most of the classes that are defined to deal with two-class problems. Therefore, in this setting, and throughout this manual, we have defined that the negatives represents the impostor attacks or false class accesses (that is when a sample of class A is given to the classifier of another class, such as class B) for of the classifier. The second set, refered as the positives represents the true class accesses or signal response of the classifier. The vectors are called this way because the procedures implemented in this module expects that the scores of negatives to be statistically distributed to the left of the signal scores (the positives). If that is not the case, one should either invert the input to the methods or multiply all scores available by -1, in order to have them inverted.

The input to create these two vectors is generated by experiments conducted by the user and normally sits in files that may need some parsing before these vectors can be extracted.

While it is not possible to provide a parser for every individual file that may be generated in different experimental frameworks, we do provide a few parsers for formats we use the most. Please refer to the documentation of bob.measure.load for a list of formats and details.

In the remainder of this section we assume you have successfuly parsed and loaded your scores in two 1D float64 vectors and are ready to evaluate the performance of the classifier.

Evaluation¶

To count the number of correctly classified positives and negatives you can use the following techniques:

>>> # negatives, positives = parse_my_scores(...) # write parser if not provided!
>>> T = 0.0 #Threshold: later we explain how one can calculate these
>>> correct_negatives = bob.measure.correctly_classified_negatives(negatives, T)
>>> FAR = 1 - (float(correct_negatives.sum())/negatives.size)
>>> correct_positives = bob.measure.correctly_classified_positives(positives, T)
>>> FRR = 1 - (float(correct_positives.sum())/positives.size)

We do provide a method to calculate the FAR and FRR in a single shot:

>>> FAR, FRR = bob.measure.farfrr(negatives, positives, T)

The threshold T is normally calculated by looking at the distribution of negatives and positives in a development (or validation) set, selecting a threshold that matches a certain criterion and applying this derived threshold to the test (or evaluation) set. This technique gives a better overview of the generalization of a method. We implement different techniques for the calculation of the threshold:

Threshold for the EER

>>> T = bob.measure.eer_threshold(negatives, positives)

Threshold for the minimum HTER

>>> T = bob.measure.min_hter_threshold(negatives, positives)

Threshold for the minimum weighted error rate (MWER) given a certain cost $\beta$ .
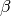```
>>> cost = 0.3 #or "beta"
>>> T = bob.measure.min_weighted_error_rate_threshold(negatives, positives, cost)
```
Note

By setting cost to 0.5 is equivalent to use bob.measure.min_hter_threshold().

Plotting¶

An image is worth 1000 words, they say. You can combine the capabilities of Matplotlib with Bob to plot a number of curves. However, you must have that package installed though. In this section we describe a few recipes.

ROC¶

The Receiver Operating Characteristic (ROC) curve is one of the oldest plots in town. To plot an ROC curve, in possession of your negatives and positives, just do something along the lines of:

>>> from matplotlib import pyplot
>>> # we assume you have your negatives and positives already split
>>> npoints = 100
>>> bob.measure.plot.roc(negatives, positives, npoints, color=(0,0,0), linestyle='-', label='test') 
>>> pyplot.xlabel('FRR (%)') 
>>> pyplot.ylabel('FAR (%)') 
>>> pyplot.grid(True)
>>> pyplot.show() 

You should see an image like the following one:

(Source code, png, hires.png, pdf)

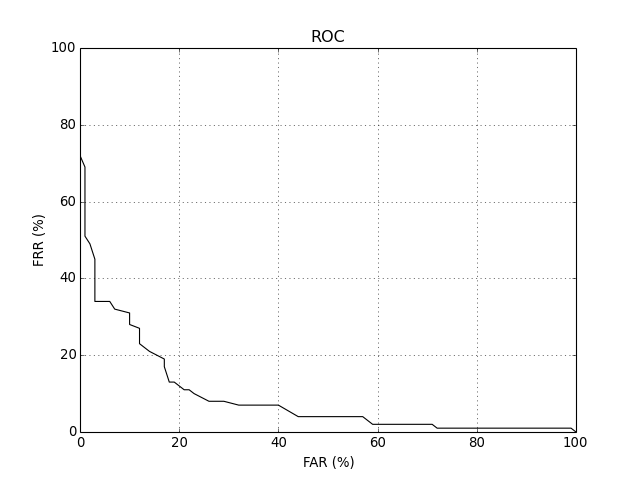
As can be observed, plotting methods live in the namespace bob.measure.plot. They work like Matplotlib‘s plot() method itself, except that instead of receiving the x and y point coordinates as parameters, they receive the two numpy.ndarray arrays with negatives and positives, as well as an indication of the number of points the curve must contain.

As in Matplotlib‘s plot() command, you can pass optional parameters for the line as shown in the example to setup its color, shape and even the label. For an overview of the keywords accepted, please refer to the Matplotlib‘s Documentation. Other plot properties such as the plot title, axis labels, grids, legends should be controlled directly using the relevant Matplotlib‘s controls.

DET¶

A DET curve can be drawn using similar commands such as the ones for the ROC curve:

>>> from matplotlib import pyplot
>>> # we assume you have your negatives and positives already split
>>> npoints = 100
>>> bob.measure.plot.det(negatives, positives, npoints, color=(0,0,0), linestyle='-', label='test') 
>>> bob.measure.plot.det_axis([0.01, 40, 0.01, 40]) 
>>> pyplot.xlabel('FAR (%)') 
>>> pyplot.ylabel('FRR (%)') 
>>> pyplot.grid(True)
>>> pyplot.show() 

This will produce an image like the following one:

(Source code, png, hires.png, pdf)

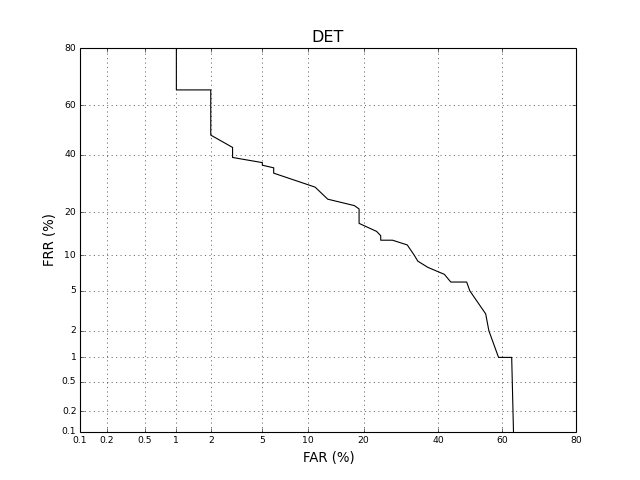
Note

If you wish to reset axis zooming, you must use the Gaussian scale rather than the visual marks showed at the plot, which are just there for displaying purposes. The real axis scale is based on the bob.measure.ppndf() method. For example, if you wish to set the x and y axis to display data between 1% and 40% here is the recipe:

>>> #AFTER you plot the DET curve, just set the axis in this way:
>>> pyplot.axis([bob.measure.ppndf(k/100.0) for k in (1, 40, 1, 40)]) 

We provide a convenient way for you to do the above in this module. So, optionally, you may use the bob.measure.plot.det_axis method like this:

>>> bob.measure.plot.det_axis([1, 40, 1, 40]) 

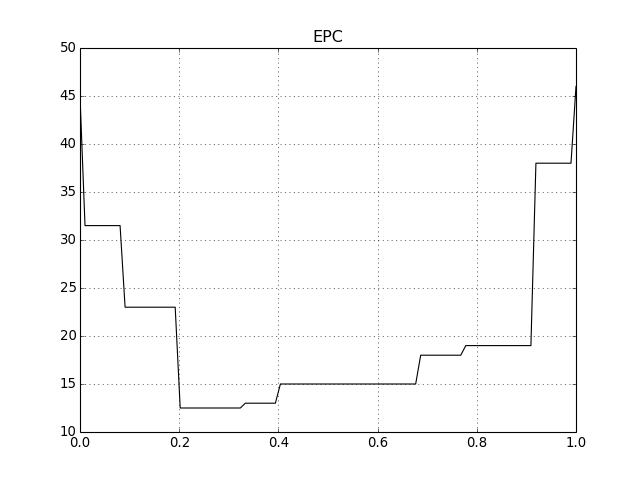
EPC¶

Drawing an EPC requires that both the development set negatives and positives are provided alognside the test (or evaluation) set ones. Because of this the API is slightly modified:

>>> bob.measure.plot.epc(dev_neg, dev_pos, test_neg, test_pos, npoints, color=(0,0,0), linestyle='-') 
>>> pyplot.show() 

This will produce an image like the following one:

(Source code, png, hires.png, pdf)

Fine-tunning¶

The methods inside bob.measure.plot are only provided as a Matplotlib wrapper to equivalent methods in bob.measure that can only calculate the points without doing any plotting. You may prefer to tweak the plotting or even use a different plotting system such as gnuplot. Have a look at the implementations at bob.measure.plot to understand how to use the Bob methods to compute the curves and interlace that in the way that best suits you.

Full applications¶

We do provide a few scripts that can be used to quickly evaluate a set of scores. We present these scripts in this section. The scripts take as input either a 4-column or 5-column data format as specified in the documentation of bob.measure.load.four_column or bob.measure.load.five_column.

To calculate the threshold using a certain criterion (EER, min.HTER or weighted Error Rate) on a set, after setting up Bob, just do:

$ bob_eval_threshold.py --scores=development-scores-4col.txt
Threshold: -0.004787956164
FAR : 6.731% (35/520)
FRR : 6.667% (26/390)
HTER: 6.699%

The output will present the threshold together with the FAR, FRR and HTER on the given set, calculated using such a threshold. The relative counts of FAs and FRs are also displayed between parenthesis.

To evaluate the performance of a new score file with a given threshold, use the application bob_apply_threshold.py:

$ bob_apply_threshold.py --scores=test-scores-4col.txt --threshold=-0.0047879
FAR : 2.115% (11/520)
FRR : 7.179% (28/390)
HTER: 4.647%

In this case, only the error figures are presented. You can conduct the evaluation and plotting of development and test set data using our combined bob_compute_perf.py script. You pass both sets and it does the rest:

$ bob_compute_perf.py --devel=development-scores-4col.txt --test=test-scores-4col.txt
[Min. criterium: EER] Threshold on Development set: -4.787956e-03
       | Development     | Test
-------+-----------------+------------------
  FAR  | 6.731% (35/520) | 2.500% (13/520)
  FRR  | 6.667% (26/390) | 6.154% (24/390)
  HTER | 6.699%          | 4.327%
[Min. criterium: Min. HTER] Threshold on Development set: 3.411070e-03
       | Development     | Test
-------+-----------------+------------------
  FAR  | 4.231% (22/520) | 1.923% (10/520)
  FRR  | 7.949% (31/390) | 7.692% (30/390)
  HTER | 6.090%          | 4.808%
[Plots] Performance curves => 'curves.pdf'

Inside that script we evaluate 2 different thresholds based on the EER and the minimum HTER on the development set and apply the output to the test set. As can be seen from the toy-example above, the system generalizes reasonably well. A single PDF file is generated containing an EPC as well as ROC and DET plots of such a system.

Use the --help option on the above-cited scripts to find-out about more options.

User Guide¶

Overview¶

Evaluation¶

Plotting¶

ROC¶

DET¶

EPC¶

Fine-tunning¶

Full applications¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

User Guide¶

Overview¶

Evaluation¶

Plotting¶

ROC¶

DET¶

EPC¶

Fine-tunning¶

Full applications¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation