Python API¶
This section includes information for using the pure Python API of bob.learn.linear.
- bob.learn.linear.get_include()[source]¶
Returns the directory containing the C/C++ API include directives
- class bob.learn.linear.CGLogRegTrainer¶
Bases: object
- CGLogRegTrainer([prior=0.5, [convergence_threshold=1e-5,
- [max_iterations=10000, [lambda=0., [mean_std_norm=False]]]]]) -> new CGLogRegTrainer
CGLogRegTrainer(other) -> new CGLogRegTrainer
Trains a linear machine to perform Linear Logistic Regression.
There are two initializers for objects of this class. In the first variant, the user passes the discrete training parameters, including the classes prior, convergence threshold and the maximum number of conjugate gradient (CG) iterations among other parameters. The second initialization form copy constructs a new trainer from an existing one.
The training stage will place the resulting weights (and bias) in a linear machine with a single output dimension. If the parameter mean_std_norm is set to True, then your input data will be mean/standard-deviation normalized and the according values will be set as normalization factors to the resulting machine.
Keyword parameters:
- prior, float (optional)
- The synthetic prior (should be in range
![]0.,1.[](../../../../_images/math/10ee9b56e0c3fbb87431121201f41fbcf2d18654.png) ).
). - convergence_threshold, float (optional)
- The convergence threshold for the conjugate gradient algorithm
- max_iterations, int (optional)
- The maximum number of iterations for the conjugate gradient algorithm
- lambda, float (optional)
- The regularization factor lambda. If you set this to the value of 0.0 (the default), then the algorithm will apply no regularization whatsoever.
- mean_std_norm, bool (optional)
- Performs mean and standard-deviation normalization (whitening) of the input data before training the (resulting) Machine. Setting this to True is recommended for large data sets with significant amplitude variations between dimensions.
- other, CGLogRegTrainer
- If you decide to copy construct from another object of the same type, pass it using this parameter.
References:
- A comparison of numerical optimizers for logistic regression, T. Minka, (See Microsoft Research paper)
- FoCal, http://www.dsp.sun.ac.za/~nbrummer/focal/
- convergence_threshold¶
The convergence threshold for the conjugate gradient algorithm
- lambda¶
The regularization factor lambda. If you set this to the value of 0.0 (the default), then the algorithm will apply no regularization whatsoever.
- max_iterations¶
The maximum number of iterations for the conjugate gradient algorithm
- mean_std_norm¶
Performs mean and standard-deviation normalization (whitening) of the input data before training the (resulting) Machine. Setting this to True is recommended for large data sets with significant amplitude variations between dimensions.
- prior¶
The synthetic prior (should be in range
![]0.,1.[](../../../../_images/math/10ee9b56e0c3fbb87431121201f41fbcf2d18654.png) ).
).
- train(negatives, positives[, machine]) → machine¶
Trains a linear machine to perform linear logistic regression.
The resulting machine will have the same number of inputs as columns in negatives and positives and a single output.
Keyword parameters:
- negatives, positives, 2D 64-bit float arrays
- These should be arrays organized in such a way that every row corresponds to a new observation of the phenomena (i.e., a new sample) and every column corresponds to a different feature.
- machine, Machine (optional)
- The user may provide or not an object of type bob.learn.linear.Machine that will be set by this method. If provided, the machine should have 1 output and the correct number of inputs matching the number of columns in the input data arrays.
This method always returns a machine, which will be the same as the one provided (if the user passed one) or a new one allocated internally.
- class bob.learn.linear.FisherLDATrainer¶
Bases: object
FisherLDATrainer([use_pinv=False [, strip_to_rank=True]]) -> new FisherLDATrainer FisherLDATrainer(other) -> new FisherLDATrainer
Trains a bob.machine.LinearMachine to perform Fisher’s Linear Discriminant Analysis (LDA).
Objects of this class can be initialized in two ways. In the first variant, the user creates a new trainer from discrete flags indicating a couple of optional parameters:
use_pinv (bool) - defaults to False
If set to True, use the pseudo-inverse to calculate
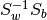 and then perform eigen value
decomposition (using LAPACK’s dgeev) instead of
using (the more numerically stable) LAPACK’s dsyvgd
to solve the generalized symmetric-definite eigenproblem
of the form
and then perform eigen value
decomposition (using LAPACK’s dgeev) instead of
using (the more numerically stable) LAPACK’s dsyvgd
to solve the generalized symmetric-definite eigenproblem
of the form 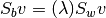 .
.Note
Using the pseudo-inverse for LDA is only recommended if you cannot make it work using the default method (via dsyvg). It is slower and requires more machine memory to store partial values of the pseudo-inverse and the dot product
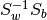 .
.strip_to_rank (bool) - defaults to True
Specifies how to calculate the final size of the to-be-trained bob.learn.linear.Machine. The default setting (True), makes the trainer return only the K-1 eigen-values/vectors limiting the output to the rank of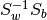 . If you set this value
to False, the it returns all eigen-values/vectors of
. If you set this value
to False, the it returns all eigen-values/vectors of
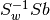 , including the ones that are supposed
to be zero.
, including the ones that are supposed
to be zero.The second initialization variant allows the user to deep copy an object of the same type creating a new identical object.
LDA finds the projection matrix W that allows us to linearly project the data matrix X to another (sub) space in which the between-class and within-class variances are jointly optimized: the between-class variance is maximized while the with-class is minimized. The (inverse) cost function for this criteria can be posed as the following:
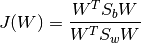
where:
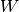 the transformation matrix that converts X into the LD space
the transformation matrix that converts X into the LD space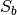 the between-class scatter; it has dimensions (X.shape[0], X.shape[0]) and is defined as
the between-class scatter; it has dimensions (X.shape[0], X.shape[0]) and is defined as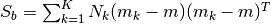 , with K
equal to the number of classes.
, with K
equal to the number of classes.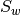 the within-class scatter; it also has dimensions (X.shape[0], X.shape[0]) and is defined as
the within-class scatter; it also has dimensions (X.shape[0], X.shape[0]) and is defined as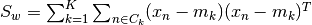 ,
with K equal to the number of classes and
,
with K equal to the number of classes and 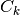 a set
representing all samples for class k.
a set
representing all samples for class k.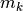 the class k empirical mean, defined as
the class k empirical mean, defined as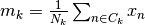
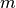 the overall set empirical mean, defined as
the overall set empirical mean, defined as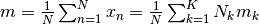
Note
A scatter matrix equals the covariance matrix if we remove the division factor.
Because this cost function is convex, you can just find its maximum by solving
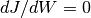 . This problem can be
re-formulated as finding the eigen values (
. This problem can be
re-formulated as finding the eigen values (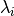 )
that solve the following condition:
)
that solve the following condition: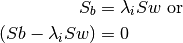
The respective eigen vectors that correspond to the eigen values
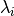 form W.
form W.- is_similar_to(other[, r_epsilon=1e-5[, a_epsilon=1e-8]]) → bool¶
Compares this FisherLDATrainer with the other one to be approximately the same.
The optional values r_epsilon and a_epsilon refer to the relative and absolute precision for the weights, biases and any other values internal to this machine.
- output_size(X) → int¶
Returns the expected size of the output (or the number of eigen-values returned) given the data.
This number could be either K-1 (where K is number of classes) or the number of columns (features) in X, depending on the setting of strip_to_rank.
This method should be used to setup linear machines and input vectors prior to feeding them into this trainer.
The value of X should be a sequence over as many 2D 64-bit floating point number arrays as classes in the problem. All arrays will be checked for conformance (identical number of columns). To accomplish this, either prepare a list with all your class observations organised in 2D arrays or pass a 3D array in which the first dimension (depth) contains as many elements as classes you want to discriminate.
- strip_to_rank¶
If the use_svd flag is enabled, this flag will indicate which LAPACK SVD function to use (dgesvd if set to True, dgesdd otherwise). By default, this flag is set to False upon construction, which makes this trainer use the fastest possible SVD decomposition.
- train(X [, machine]) -> (machine, eigen_values)¶
Trains a given machine to perform Fisher/LDA discrimination.
After this method has been called, an input machine (or one allocated internally) will have the eigen-vectors of the
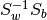 product, arranged by decreasing energy.
Each input data set represents data from a given input class.
This method also returns the eigen values allowing you to
implement your own compression scheme.
product, arranged by decreasing energy.
Each input data set represents data from a given input class.
This method also returns the eigen values allowing you to
implement your own compression scheme.The user may provide or not an object of type bob.learn.linear.Machine that will be set by this method. If provided, machine should have the correct number of inputs and outputs matching, respectively, the number of columns in the input data arrays X and the output of the method bob.learn.linear.FisherLDATrainer.output_size() (see help).
The value of X should be a sequence over as many 2D 64-bit floating point number arrays as classes in the problem. All arrays will be checked for conformance (identical number of columns). To accomplish this, either prepare a list with all your class observations organised in 2D arrays or pass a 3D array in which the first dimension (depth) contains as many elements as classes you want to discriminate.
Note
We set at most bob.trainer.FisherLDATrainer.output_size() eigen-values and vectors on the passed machine. You can compress the machine output further using bob.learn.linear.Machine.resize() if necessary.
- use_pinv¶
If True, use the pseudo-inverse to calculate
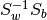 and then perform the eigen value
decomposition (using LAPACK’s dgeev) instead of using
(the more numerically stable) LAPACK’s dsyvgd to solve
the generalized symmetric-definite eigenproblem of the
form
and then perform the eigen value
decomposition (using LAPACK’s dgeev) instead of using
(the more numerically stable) LAPACK’s dsyvgd to solve
the generalized symmetric-definite eigenproblem of the
form 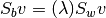
- class bob.learn.linear.Machine¶
Bases: object
Machine([input_size=0, [output_size=0]]) Machine(weights) Machine(config) Machine(other)
A linear classifier. See C. M. Bishop, ‘Pattern Recognition and Machine Learning’, chapter 4 for more details. The basic matrix operation performed for projecting the input to the output is:
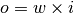 (with
(with 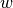 being the
vector of machine weights and
being the
vector of machine weights and 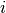 the input data vector).
The weights matrix is therefore organized column-wise. In this
scheme, each column of the weights matrix can be interpreted
as vector to which the input is projected. The number of
columns of the weights matrix determines the number of outputs
this linear machine will have. The number of rows, the number
of allowed inputs it can process.
the input data vector).
The weights matrix is therefore organized column-wise. In this
scheme, each column of the weights matrix can be interpreted
as vector to which the input is projected. The number of
columns of the weights matrix determines the number of outputs
this linear machine will have. The number of rows, the number
of allowed inputs it can process.Input and output is always performed on 1D arrays with 64-bit floating point numbers.
A linear machine can be constructed in different ways. In the first form, the user specifies optional input and output vector sizes. The machine is remains uninitialized. With the second form, the user passes a 2D array with 64-bit floats containing weight matrix to be used by the new machine. In the third form the user passes a pre-opened HDF5 file pointing to the machine information to be loaded in memory. Finally, in the last form (copy constructor), the user passes another Machine that will be fully copied.
- activation¶
The activation function - by default, the identity function. The output provided by the activation function is passed, unchanged, to the user.
- biases¶
Bias to the output units of this linear machine, to be added to the output before activation.
- forward(input[, output]) → array¶
Projects input through its internal weights and biases. If output is provided, place output there instead of allocating a new array.
The input (and output) arrays can be either 1D or 2D 64-bit float arrays. If one provides a 1D array, the output array, if provided, should also be 1D, matching the output size of this machine. If one provides a 2D array, it is considered a set of vertically stacked 1D arrays (one input per row) and a 2D array is produced or expected in output. The output array in this case shall have the same number of rows as the input array and as many columns as the output size for this machine.
Note
This method only accepts 64-bit float arrays as input or output.
- input_divide¶
Input division factor, before feeding data through the weight matrix W. The division is applied just after subtraction - by default, it is set to 1.0.
- input_subtract¶
Input subtraction factor, before feeding data through the weight matrix W. The subtraction is the first applied operation in the processing chain - by default, it is set to 0.0.
- is_similar_to(other[, r_epsilon=1e-5[, a_epsilon=1e-8]]) → bool¶
Compares this LinearMachine with the other one to be approximately the same.
The optional values r_epsilon and a_epsilon refer to the relative and absolute precision for the weights, biases and any other values internal to this machine.
- load(f) → None¶
Loads itself from a bob.io.HDF5File
- resize(input, output) → None¶
Resizes the machine. If either the input or output increases in size, the weights and other factors should be considered uninitialized. If the size is preserved or reduced, already initialized values will not be changed.
Note
Use this method to force data compression. All will work out given most relevant factors to be preserved are organized on the top of the weight matrix. In this way, reducing the system size will supress less relevant projections.
- save(f) → None¶
Saves itself at a bob.io.HDF5File
- shape¶
A tuple that represents the size of the input vector followed by the size of the output vector in the format (input, output).
- weights¶
Weight matrix to which the input is projected to. The output of the project is fed subject to bias and activation before being output.
- class bob.learn.linear.PCATrainer¶
Bases: object
PCATrainer([use_svd=True]) -> new PCATrainer
PCATrainer(other) -> new PCATrainer
Sets a linear machine to perform the Principal Component Analysis (a.k.a. Karhunen-Loeve Transform) on a given dataset using either Singular Value Decomposition (SVD, the default) or the Covariance Matrix Method.
The training stage will place the resulting principal components in the linear machine and set it up to extract the variable means automatically. As an option, you may preset the trainer so that the normalization performed by the resulting linear machine also divides the variables by the standard deviation of each variable ensemble.
There are two initializers for objects of this class. In the first variant, the user can pass a flag indicating if the trainer should use SVD (default) or the covariance method for PCA extraction. The second initialization form copy constructs a new trainer from an existing one.
The principal components correspond the direction of the data in which its points are maximally spread.
Computing these principal components is equivalent to computing the eigen vectors U for the covariance matrix Sigma extracted from the data matrix X. The covariance matrix for the data is computed using the equation below:
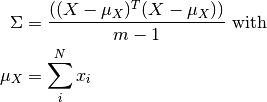
where
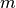 is the number of rows in
is the number of rows in 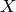 (that is,
the number of samples).
(that is,
the number of samples).Once you are in possession of
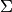 , it suffices
to compute the eigen vectors U, solving the linear equation:
, it suffices
to compute the eigen vectors U, solving the linear equation: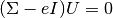
In this trainer, we make use of LAPACK’s dsyevd to solve the above equation, if you choose to use the Covariance Method for extracting the principal components of your data matrix
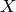 .
.By default though, this class will perform PC extraction using SVD. SVD is a factorization technique that allows for the decomposition of a matrix
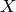 , with size (m,n) into
3 other matrices in this way:
, with size (m,n) into
3 other matrices in this way: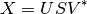
where:
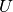
- unitary matrix of size (m,m) - a.k.a., left singular vectors of X
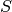
- rectangular diagonal matrix with nonnegative real numbers, size (m,n)
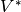
- (the conjugate transpose of V) unitary matrix of size (n,n), a.k.a. right singular vectors of X
We can use this property to avoid the computation of the covariance matrix of the data matrix
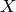 , if we note
the following:
, if we note
the following: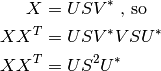
If X has zero mean, we can conclude by inspection that the U matrix obtained by SVD contains the eigen vectors of the covariance matrix of X (
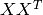 ) and
) and 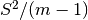 corresponds to its eigen values.
corresponds to its eigen values.Note
Our implementation uses LAPACK’s dgesdd to compute the solution to this linear equation.
The corresponding bob.learn.Linear.Machine and returned eigen-values of
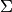 , are pre-sorted in
descending order (the first eigen-vector - or column - of the
weight matrix in the bob.learn.Linear.Machine
corresponds to the highest eigen value obtained).
, are pre-sorted in
descending order (the first eigen-vector - or column - of the
weight matrix in the bob.learn.Linear.Machine
corresponds to the highest eigen value obtained).Note
One question you should pose yourself is which of the methods to choose. Here is some advice: you should prefer the covariance method over SVD when the number of samples (rows of
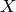 ) is greater than the number of features
(columns of
) is greater than the number of features
(columns of 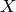 ). It provides a faster execution
path in that case. Otherwise, use the default SVD method.
). It provides a faster execution
path in that case. Otherwise, use the default SVD method.References:
- Eigenfaces for Recognition, Turk & Pentland, Journal of Cognitive Neuroscience (1991) Volume: 3, Issue: 1, Publisher: MIT Press, Pages: 71-86
- http://en.wikipedia.org/wiki/Singular_value_decomposition
- http://en.wikipedia.org/wiki/Principal_component_analysis
- http://www.netlib.org/lapack/double/dsyevd.f
- http://www.netlib.org/lapack/double/dgesdd.f
- is_similar_to(other[, r_epsilon=1e-5[, a_epsilon=1e-8]]) → bool¶
Compares this PCATrainer with the other one to be approximately the same.
The optional values r_epsilon and a_epsilon refer to the relative and absolute precision for the weights, biases and any other values internal to this machine.
- output_size(X) → int¶
Calculates the maximum possible rank for the covariance matrix of X, given X.
Returns the maximum number of non-zero eigen values that can be generated by this trainer, given some data. This number (K) depends on the size of X and is calculated as follows
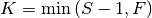 , with
, with 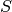 being the
number of rows in data (samples) and
being the
number of rows in data (samples) and 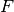 the
number of columns (or features).
the
number of columns (or features).This method should be used to setup linear machines and input vectors prior to feeding them into this trainer.
- safe_svd¶
If the use_svd flag is enabled, this flag will indicate which LAPACK SVD function to use (dgesvd if set to True, dgesdd otherwise). By default, this flag is set to False upon construction, which makes this trainer use the fastest possible SVD decomposition.
- train(X [, machine]) -> (machine, eigen_values)¶
Trains a linear machine to perform the KLT.
The resulting machine will have the same number of inputs as columns in X and
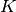 eigen-vectors, where
eigen-vectors, where
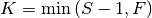 , with
, with 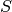 being the number of
rows in X (samples) and
being the number of
rows in X (samples) and 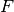 the number of columns
(or features). The vectors are arranged by decreasing
eigen-value automatically. You don’t need to sort the results.
the number of columns
(or features). The vectors are arranged by decreasing
eigen-value automatically. You don’t need to sort the results.The user may provide or not an object of type bob.learn.linear.Machine that will be set by this method. If provided, machine should have the correct number of inputs and outputs matching, respectively, the number of columns in the input data array X and the output of the method bob.learn.linear.PCATrainer.output_size() (see help).
The input data matrix
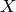 should correspond to a 64-bit
floating point array organized in such a way that every row
corresponds to a new observation of the phenomena (i.e., a new
sample) and every column corresponds to a different feature.
should correspond to a 64-bit
floating point array organized in such a way that every row
corresponds to a new observation of the phenomena (i.e., a new
sample) and every column corresponds to a different feature.This method returns a tuple consisting of the trained machine and a 1D 64-bit floating point array containing the eigen-values calculated while computing the KLT. The eigen-value ordering matches that of eigen-vectors set in the machine.
- use_svd¶
This flag determines if this trainer will use the SVD method (set it to True) to calculate the principal components or the Covariance method (set it to False).
- class bob.learn.linear.WCCNTrainer¶
Bases: object
WCCNTrainer() -> new WCCNTrainer
Trains a linear machine to perform Within-Class Covariance Normalisation (WCCN).
WCCN finds the projection matrix W that allows us to linearly project the data matrix X to another (sub) space such that:
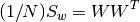
where W is an upper triangular matrix computed using Cholesky Decomposition:
![W = cholesky([(1/K) S_{w} ]^{-1})](../../../../_images/math/f847f66c86552ce2b007018ebcaeeff1c2b61d76.png)
where:
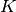 the number of classes
the number of classes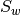 the within-class scatter; it also has dimensions (X.shape[0], X.shape[0]) and is defined as
the within-class scatter; it also has dimensions (X.shape[0], X.shape[0]) and is defined as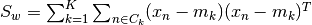 ,
,
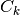 a set representing all samples for class k.
a set representing all samples for class k.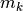 the class k empirical mean, defined as
the class k empirical mean, defined as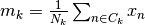
References:
- Andrew O. Hatch, Sachin Kajarekar, and Andreas Stolcke, Within-class covariance normalization for SVM-based speaker recognition, In INTERSPEECH, 2006.
- http://en.wikipedia.org/wiki/Cholesky_decomposition
- is_similar_to(other[, r_epsilon=1e-5[, a_epsilon=1e-8]]) → bool¶
Compares this WCCNTrainer with the other one to be approximately the same.
The optional values r_epsilon and a_epsilon refer to the relative and absolute precision for the weights, biases and any other values internal to this machine.
- train(X[, machine]) → machine¶
Trains a linear machine using WCCN.
The resulting machine will have the same number of inputs and outputs as columns in any of X‘s matrices.
The user may provide or not an object of type bob.learn.linear.Machine that will be set by this method. In such a case, the machine should have a shape that matches (X.shape[1], X.shape[1]). If the user does not provide a machine to be set, then a new one will be allocated internally. In both cases, the resulting machine is always returned by this method.
The value of X should be a sequence over as many 2D 64-bit floating point number arrays as classes in the problem. All arrays will be checked for conformance (identical number of columns). To accomplish this, either prepare a list with all your class observations organised in 2D arrays or pass a 3D array in which the first dimension (depth) contains as many elements as classes you want to train for.
- class bob.learn.linear.WhiteningTrainer¶
Bases: object
WhiteningTrainer() -> new WhiteningTrainer
Trains a linear machine` to perform Cholesky Whitening.
The whitening transformation is a decorrelation method that converts the covariance matrix of a set of samples into the identity matrix
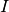 . This effectively linearly transforms random variables such
that the resulting variables are uncorrelated and have the same
variances as the original random variables. This transformation is
invertible. The method is called the whitening transform because it
transforms the input matrix X closer towards white noise (let’s call
it
. This effectively linearly transforms random variables such
that the resulting variables are uncorrelated and have the same
variances as the original random variables. This transformation is
invertible. The method is called the whitening transform because it
transforms the input matrix X closer towards white noise (let’s call
it 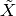 ):
):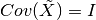
where:
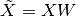
W is the projection matrix that allows us to linearly project the data matrix X to another (sub) space such that:
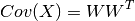
W is computed using Cholesky Decomposition:
![W = cholesky([Cov(X)]^{-1})](../../../../_images/math/63ca1fadadaa98eaea4ce19c32a9cd4e836273cc.png)
References:
- https://rtmath.net/help/html/e9c12dc0-e813-4ca9-aaa3-82340f1c5d24.htm
- http://en.wikipedia.org/wiki/Cholesky_decomposition
- is_similar_to(other[, r_epsilon=1e-5[, a_epsilon=1e-8]]) → bool¶
Compares this WhiteningTrainer with the other one to be approximately the same.
The optional values r_epsilon and a_epsilon refer to the relative and absolute precision for the weights, biases and any other values internal to this machine.
- train(X[, machine]) → machine¶
The resulting machine will have the same number of inputs and outputs as columns in X.
The user may provide or not an object of type bob.learn.linear.Machine that will be set by this method. In such a case, the machine should have a shape that matches (X.shape[1], X.shape[1]). If the user does not provide a machine to be set, then a new one will be allocated internally. In both cases, the resulting machine is always returned by this method.
The input data matrix
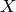 should correspond to a 64-bit
floating point 2D array organized in such a way that every row
corresponds to a new observation of the phenomena (i.e., a new
sample) and every column corresponds to a different feature.
should correspond to a 64-bit
floating point 2D array organized in such a way that every row
corresponds to a new observation of the phenomena (i.e., a new
sample) and every column corresponds to a different feature.