Python API¶
This section includes information for using the pure Python API of bob.math.
Summary¶
| bob.math.LPInteriorPoint | Base class to solve a linear program using interior point methods. |
| bob.math.LPInteriorPointShortstep | A Linear Program solver based on a short step interior point method. |
| bob.math.LPInteriorPointLongstep | A Linear Program solver based on a long step interior point method. |
Details¶
- class bob.math.LPInteriorPoint¶
Bases: object
Base class to solve a linear program using interior point methods.
For more details about the algorithms,please refer to the following book: ‘Primal-Dual Interior-Point Methods’, Stephen J. Wright, ISBN: 978-0898713824, Chapter 5, ‘Path-Following Algorithms’.
Warning
You cannot instantiate an object of this type directly, you must use it through one of the inherited types.
The primal linear program (LP) is defined as follows:
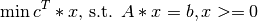
The dual formulation is:

Class Members:
- epsilon¶
float <– The precision to determine whether an equality constraint is fulfilled or not
- initialize_dual_lambda_mu(A, c) → None¶
Initializes the dual variables lambda and mu by minimizing the logarithmic barrier function.
Todo
The parameter(s) ‘A, c’ are used, but not documented.
- is_feasible(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the set of feasible points (i.e. fulfills the constraints).
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the set of feasible points, otherwise False
- is_in_v(x, mu, theta) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the V2 neighborhood of the central path.
Todo
This documentation seems wrong since lambda is not in the list of parameters.
Todo
The parameter(s) ‘mu, theta, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V2 neighborhood of the central path, otherwise False
- is_in_v_s(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x,lambda,mu) belongs to the V neighborhood of the central path and the set of feasible points.
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V neighborhood of the central path and the set of feasible points, otherwise False
- lambda_¶
float <– The value of the
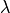 dual variable (read-only)
dual variable (read-only)
- m¶
int <– The first dimension of the problem/A matrix
- mu¶
float <– The value of the
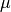 dual variable (read-only)
dual variable (read-only)
- n¶
int <– The second dimension of the problem/A matrix
- reset(M, N) → None¶
Resets the size of the problem (M and N correspond to the dimensions of the A matrix)
Parameters:
M : int
The new first dimension of the problem/A matrixN : int
The new second dimension of the problem/A matrix
- solve(A, b, c, x0, lambda, mu) → x¶
Solves an LP problem
Todo
The parameter(s) ‘A, b, c, x0’ are used, but not documented.
Todo
The return value(s) ‘x’ are used, but not documented.
Parameters:
lambda : ?, optional
Todo
Document parameter labmda
mu : ?, optional
Todo
Document parameter mu
- class bob.math.LPInteriorPointLongstep¶
Bases: bob.math.LPInteriorPoint
A Linear Program solver based on a long step interior point method.
See LPInteriorPoint for more details on the base class.
Constructor Documentation:
- bob.math.LPInteriorPointLongstep (M, N, gamma, sigma, epsilon)
- bob.math.LPInteriorPointLongstep (solver)
Objects of this class can be initialized in two different ways: a detailed constructor with the parameters described below or a copy constructor, that deep-copies the input object and creates a new object (not a new reference to the same object)
Parameters:
M : int
first dimension of the A matrixN : int
second dimension of the A matrixgamma : float
the value gamma used to define a V-inf neighborhoodsigma : float
the value sigma used to define a V-inf neighborhoodepsilon : float
the precision to determine whether an equality constraint is fulfilled or notsolver : LPInteriorPointLongstep
the solver to make a deep copy ofClass Members:
- epsilon¶
float <– The precision to determine whether an equality constraint is fulfilled or not
- gamma¶
float <– The value gamma used to define a V-Inf neighborhood
- initialize_dual_lambda_mu(A, c) → None¶
Initializes the dual variables lambda and mu by minimizing the logarithmic barrier function.
Todo
The parameter(s) ‘A, c’ are used, but not documented.
- is_feasible(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the set of feasible points (i.e. fulfills the constraints).
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the set of feasible points, otherwise False
- is_in_v(x, mu, gamma) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the V-Inf neighborhood of the central path.
Todo
This documentation looks wrong since lambda is not part of the parameters
Todo
The parameter(s) ‘gamma, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, lambda, mu) belong to the V-Inf neighborhood of the central path, otherwise False
- is_in_v_s(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x,lambda,mu) belongs to the V neighborhood of the central path and the set of feasible points.
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V neighborhood of the central path and the set of feasible points, otherwise False
- lambda_¶
float <– The value of the
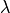 dual variable (read-only)
dual variable (read-only)
- m¶
int <– The first dimension of the problem/A matrix
- mu¶
float <– The value of the
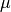 dual variable (read-only)
dual variable (read-only)
- n¶
int <– The second dimension of the problem/A matrix
- reset(M, N) → None¶
Resets the size of the problem (M and N correspond to the dimensions of the A matrix)
Parameters:
M : int
The new first dimension of the problem/A matrixN : int
The new second dimension of the problem/A matrix
- sigma¶
float <– The value sigma used to define a V-Inf neighborhood
- solve(A, b, c, x0, lambda, mu) → x¶
Solves an LP problem
Todo
The parameter(s) ‘A, b, c, x0’ are used, but not documented.
Todo
The return value(s) ‘x’ are used, but not documented.
Parameters:
lambda : ?, optional
Todo
Document parameter labmda
mu : ?, optional
Todo
Document parameter mu
- class bob.math.LPInteriorPointPredictorCorrector¶
Bases: bob.math.LPInteriorPoint
A Linear Program solver based on a predictor-corrector interior point method.
See LPInteriorPoint for more details on the base class.
Constructor Documentation:
- bob.math.LPInteriorPointPredictorCorrector (M, N, theta_pred, theta_corr, epsilon)
- bob.math.LPInteriorPointPredictorCorrector (solver)
Objects of this class can be initialized in two different ways: a detailed constructor with the parameters described below or a copy constructor, that deep-copies the input object and creates a new object (not a new reference to the same object).
Parameters:
M : int
first dimension of the A matrixN : int
second dimension of the A matrixtheta_pred : float
the value theta_pred used to define a V2 neighborhoodtheta_corr : float
the value theta_corr used to define a V2 neighborhoodepsilon : float
the precision to determine whether an equality constraint is fulfilled or notsolver : LPInteriorPointPredictorCorrector
the solver to make a deep copy ofClass Members:
- epsilon¶
float <– The precision to determine whether an equality constraint is fulfilled or not
- initialize_dual_lambda_mu(A, c) → None¶
Initializes the dual variables lambda and mu by minimizing the logarithmic barrier function.
Todo
The parameter(s) ‘A, c’ are used, but not documented.
- is_feasible(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the set of feasible points (i.e. fulfills the constraints).
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the set of feasible points, otherwise False
- is_in_v(x, mu, theta) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the V2 neighborhood of the central path.
Todo
This documentation seems wrong since lambda is not in the list of parameters.
Todo
The parameter(s) ‘mu, theta, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V2 neighborhood of the central path, otherwise False
- is_in_v_s(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x,lambda,mu) belongs to the V neighborhood of the central path and the set of feasible points.
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V neighborhood of the central path and the set of feasible points, otherwise False
- lambda_¶
float <– The value of the
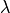 dual variable (read-only)
dual variable (read-only)
- m¶
int <– The first dimension of the problem/A matrix
- mu¶
float <– The value of the
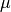 dual variable (read-only)
dual variable (read-only)
- n¶
int <– The second dimension of the problem/A matrix
- reset(M, N) → None¶
Resets the size of the problem (M and N correspond to the dimensions of the A matrix)
Parameters:
M : int
The new first dimension of the problem/A matrixN : int
The new second dimension of the problem/A matrix
- solve(A, b, c, x0, lambda, mu) → x¶
Solves an LP problem
Todo
The parameter(s) ‘A, b, c, x0’ are used, but not documented.
Todo
The return value(s) ‘x’ are used, but not documented.
Parameters:
lambda : ?, optional
Todo
Document parameter labmda
mu : ?, optional
Todo
Document parameter mu
- theta_corr¶
float <– The value theta_corr used to define a V2 neighborhood
- theta_pred¶
float <– The value theta_pred used to define a V2 neighborhood
- class bob.math.LPInteriorPointShortstep¶
Bases: bob.math.LPInteriorPoint
A Linear Program solver based on a short step interior point method. See LPInteriorPoint for more details on the base class.
Constructor Documentation:
- bob.math.LPInteriorPointShortstep (M, N, theta, epsilon)
- bob.math.LPInteriorPointShortstep (solver)
Objects of this class can be initialized in two different ways: a detailed constructor with the parameters described below or a copy constructor that deep-copies the input object and creates a new object (not a new reference to the same object).
Parameters:
M : int
first dimension of the A matrixN : int
second dimension of the A matrixtheta : float
The value defining the size of the V2 neighborhoodepsilon : float
The precision to determine whether an equality constraint is fulfilled or not.solver : LPInteriorPointShortstep
The solver to make a deep copy ofClass Members:
- epsilon¶
float <– The precision to determine whether an equality constraint is fulfilled or not
- initialize_dual_lambda_mu(A, c) → None¶
Initializes the dual variables lambda and mu by minimizing the logarithmic barrier function.
Todo
The parameter(s) ‘A, c’ are used, but not documented.
- is_feasible(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the set of feasible points (i.e. fulfills the constraints).
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the set of feasible points, otherwise False
- is_in_v(x, mu, theta) → test¶
Checks if a primal-dual point (x, lambda, mu) belongs to the V2 neighborhood of the central path.
Todo
This documentation seems wrong since lambda is not in the list of parameters.
Todo
The parameter(s) ‘mu, theta, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V2 neighborhood of the central path, otherwise False
- is_in_v_s(A, b, c, x, lambda, mu) → test¶
Checks if a primal-dual point (x,lambda,mu) belongs to the V neighborhood of the central path and the set of feasible points.
Todo
The parameter(s) ‘A, b, c, lambda, mu, x’ are used, but not documented.
Returns:
test : bool
True if (x, labmda, mu) belongs to the V neighborhood of the central path and the set of feasible points, otherwise False
- lambda_¶
float <– The value of the
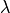 dual variable (read-only)
dual variable (read-only)
- m¶
int <– The first dimension of the problem/A matrix
- mu¶
float <– The value of the
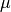 dual variable (read-only)
dual variable (read-only)
- n¶
int <– The second dimension of the problem/A matrix
- reset(M, N) → None¶
Resets the size of the problem (M and N correspond to the dimensions of the A matrix)
Parameters:
M : int
The new first dimension of the problem/A matrixN : int
The new second dimension of the problem/A matrix
- solve(A, b, c, x0, lambda, mu) → x¶
Solves an LP problem
Todo
The parameter(s) ‘A, b, c, x0’ are used, but not documented.
Todo
The return value(s) ‘x’ are used, but not documented.
Parameters:
lambda : ?, optional
Todo
Document parameter labmda
mu : ?, optional
Todo
Document parameter mu
- theta¶
float <– The value theta used to define a V2 neighborhood
- bob.math.chi_square()¶
- chi_square(h1, h2) -> dist
- chi_square(index_1, value_1, index_2, value_2) -> dist
Computes the chi square distance between the given histograms, which might be of singular dimension only.
The chi square distance is computed as follows:
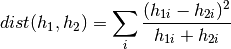
Chi square defines a distance metric, so lower values are better. You can use this method in two different formats. The first interface accepts non-sparse histograms. The second interface accepts sparse histograms represented by indexes and values.
Note
Histograms are given as two matrices, one with the indexes and one with the data. All data points that for which no index exists are considered to be zero.
Note
In general, histogram intersection with sparse histograms needs more time to be computed.
Parameters:
h1, h2 : array_like (1D)
Histograms to compute the chi square distance forindex_1, index_2 : array_like (int, 1D)
Indices of the sparse histograms value_1 and value_2value_1, value_2 : array_like (1D)
Sparse histograms to compute the chi square distance forReturns:
dist : float
The chi square distance value for the given histograms.
- bob.math.histogram_intersection()¶
- histogram_intersection(h1, h2) -> sim
- histogram_intersection(index_1, value_1, index_2, value_2) -> sim
Computes the histogram intersection between the given histograms, which might be of singular dimension only.
The histogram intersection is computed as follows:
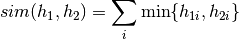
The histogram intersection defines a similarity measure, so higher values are better. You can use this method in two different formats. The first interface accepts non-sparse histograms. The second interface accepts sparse histograms represented by indexes and values.
Note
Histograms are given as two matrices, one with the indexes and one with the data. All data points that for which no index exists are considered to be zero.
Note
In general, histogram intersection with sparse histograms needs more time to be computed.
Parameters:
h1, h2 : array_like (1D)
Histograms to compute the histogram intersection forindex_1, index_2 : array_like (int, 1D)
Indices of the sparse histograms value_1 and value_2value_1, value_2 : array_like (1D)
Sparse histograms to compute the histogram intersection forReturns:
sim : float
The histogram intersection value for the given histograms.
- bob.math.kullback_leibler()¶
- kullback_leibler(h1, h2) -> dist
- kullback_leibler(index_1, value_1, index_2, value_2) -> dist
Computes the Kullback-Leibler histogram divergence between the given histograms, which might be of singular dimension only.
The chi square distance is inspired by link and computed as follows:
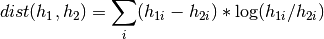
The Kullback-Leibler divergence defines a distance metric, so lower values are better. You can use this method in two different formats. The first interface accepts non-sparse histograms. The second interface accepts sparse histograms represented by indexes and values.
Note
Histograms are given as two matrices, one with the indexes and one with the data. All data points that for which no index exists are considered to be zero.
Note
In general, histogram intersection with sparse histograms needs more time to be computed.
Parameters:
h1, h2 : array_like (1D)
Histograms to compute the Kullback-Leibler divergence forindex_1, index_2 : array_like (int, 1D)
Indices of the sparse histograms value_1 and value_2value_1, value_2 : array_like (1D)
Sparse histograms to compute the Kullback-Leibler divergence forReturns:
dist : float
The Kullback-Leibler divergence value for the given histograms.
- bob.math.linsolve()¶
- linsolve(A, b) -> x
- linsolve(A, b, x) -> None
Solves the linear system
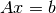 and returns the result in
and returns the result in
 .
.This method uses LAPACK’s dgesv generic solver. You can use this method in two different formats. The first interface accepts the matrices
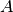 and
and 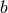 returning
returning  . The second one
accepts a pre-allocated
. The second one
accepts a pre-allocated  vector and sets it with the linear
system solution.
vector and sets it with the linear
system solution.Parameters:
A : array_like (2D)
The matrix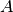 of the linear system
of the linear systemb : array_like (1D)
The vector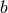 of the linear system
of the linear systemx : array_like (1D)
The result vector , as parameter
, as parameterReturns:
x : array_like (1D)
The result vector , as return value
, as return value
- bob.math.linsolve_()¶
- linsolve_(A, b) -> x
- linsolve_(A, b, x) -> None
Solves the linear system
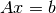 and returns the result in
and returns the result in
 .
.Warning
This variant does not perform any checks on the input matrices and is faster then linsolve(). Use it when you are sure your input matrices sizes match.
This method uses LAPACK’s dgesv generic solver. You can use this method in two different formats. The first interface accepts the matrices
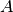 and
and 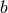 returning
returning  . The second one
accepts a pre-allocated
. The second one
accepts a pre-allocated  vector and sets it with the linear
system solution.
vector and sets it with the linear
system solution.Parameters:
A : array_like (2D)
The matrix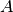 of the linear system
of the linear systemb : array_like (1D)
The vector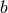 of the linear system
of the linear systemx : array_like (1D)
The result vector , as parameter
, as parameterReturns:
x : array_like (1D)
The result vector , as return value
, as return value
- bob.math.linsolve_cg_sympos()¶
- linsolve_cg_sympos(A, b) -> x
- linsolve_cg_sympos(A, b, x) -> None
Solves the linear system
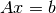 using conjugate gradients and
returns the result in
using conjugate gradients and
returns the result in  for symmetric
for symmetric 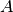 matrix.
matrix.This method uses the conjugate gradient solver, assuming
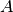 is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices
is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices 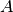 and
and 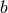 returning
returning  . The second one accepts a
pre-allocated
. The second one accepts a
pre-allocated  vector and sets it with the linear system
solution.
vector and sets it with the linear system
solution.Parameters:
A : array_like (2D)
The matrix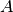 of the linear system
of the linear systemb : array_like (1D)
The vector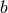 of the linear system
of the linear systemx : array_like (1D)
The result vector , as parameter
, as parameterReturns:
x : array_like (1D)
The result vector , as return value
, as return value
- bob.math.linsolve_cg_sympos_()¶
- linsolve_cg_sympos_(A, b) -> x
- linsolve_cg_sympos_(A, b, x) -> None
Solves the linear system
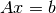 using conjugate gradients and
returns the result in
using conjugate gradients and
returns the result in  for symmetric
for symmetric 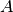 matrix.
matrix.Warning
This variant does not perform any checks on the input matrices and is faster then linsolve_cg_sympos(). Use it when you are sure your input matrices sizes match.
This method uses the conjugate gradient solver, assuming
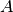 is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices
is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices 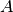 and
and 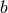 returning
returning  . The second one accepts a
pre-allocated
. The second one accepts a
pre-allocated  vector and sets it with the linear system
solution.
vector and sets it with the linear system
solution.Parameters:
A : array_like (2D)
The matrix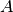 of the linear system
of the linear systemb : array_like (1D)
The vector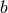 of the linear system
of the linear systemx : array_like (1D)
The result vector , as parameter
, as parameterReturns:
x : array_like (1D)
The result vector , as return value
, as return value
- bob.math.linsolve_sympos()¶
- linsolve_sympos(A, b) -> x
- linsolve_sympos(A, b, x) -> None
Solves the linear system
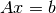 and returns the result in
and returns the result in
 for symmetric
for symmetric 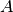 matrix.
matrix.This method uses LAPACK’s dposv solver, assuming
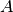 is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices
is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices 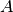 and
and 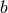 returning
returning  . The second one accepts a
pre-allocated
. The second one accepts a
pre-allocated  vector and sets it with the linear system
solution.
vector and sets it with the linear system
solution.Parameters:
A : array_like (2D)
The matrix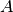 of the linear system
of the linear systemb : array_like (1D)
The vector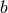 of the linear system
of the linear systemx : array_like (1D)
The result vector , as parameter
, as parameterReturns:
x : array_like (1D)
The result vector , as return value
, as return value
- bob.math.linsolve_sympos_()¶
- linsolve_sympos_(A, b) -> x
- linsolve_sympos_(A, b, x) -> None
Solves the linear system
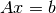 and returns the result in
and returns the result in
 for symmetric
for symmetric 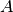 matrix.
matrix.Warning
This variant does not perform any checks on the input matrices and is faster then linsolve_sympos(). Use it when you are sure your input matrices sizes match.
This method uses LAPACK’s dposv solver, assuming
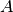 is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices
is a
symmetric positive definite matrix. You can use this method in two
different formats. The first interface accepts the matrices 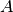 and
and 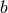 returning
returning  . The second one accepts a
pre-allocated
. The second one accepts a
pre-allocated  vector and sets it with the linear system
solution.
vector and sets it with the linear system
solution.Parameters:
A : array_like (2D)
The matrix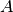 of the linear system
of the linear systemb : array_like (1D)
The vector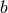 of the linear system
of the linear systemx : array_like (1D)
The result vector , as parameter
, as parameterReturns:
x : array_like (1D)
The result vector , as return value
, as return value
- bob.math.norminv(p, mu, sigma) → inv¶
Computes the inverse normal cumulative distribution
Computes the inverse normal cumulative distribution for a probability
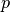 , given a distribution with mean
, given a distribution with mean 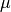 and standard
deviation
and standard
deviation 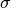 . Reference:
http://home.online.no/~pjacklam/notes/invnorm/
. Reference:
http://home.online.no/~pjacklam/notes/invnorm/Parameters:
p : float
The value to get the inverse distribution of, must lie in the range![[0,1]](../../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png)
mu : float
The mean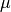 of the normal distribution
of the normal distributionsigma : float
The standard deviation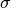 of the normal distribution
of the normal distributionReturns:
inv : float
The inverse of the normal distribution
- bob.math.normsinv(p) → inv¶
Computes the inverse normal cumulative distribution
Computes the inverse normal cumulative distribution for a probability
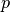 , given a distribution with mean
, given a distribution with mean 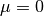 and standard
deviation
and standard
deviation  . It is equivalent as calling norminv(p, 0,
1) (see norminv()). Reference:
http://home.online.no/~pjacklam/notes/invnorm/
. It is equivalent as calling norminv(p, 0,
1) (see norminv()). Reference:
http://home.online.no/~pjacklam/notes/invnorm/Parameters:
p : float
The value to get the inverse distribution of, must lie in the range![[0,1]](../../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png)
Returns:
inv : float
The inverse of the normal distribution
- bob.math.pavx()¶
- pavx(input, output) -> None
- pavx(input) -> output
Applies the Pool-Adjacent-Violators Algorithm
Applies the Pool-Adjacent-Violators Algorithm to input. This is a simplified C++ port of the isotonic regression code made available at the University of Bern website.
You can use this method in two different formats. The first interface accepts the input and output. The second one accepts the input array input and allocates a new output array, which is returned.
Parameters:
input : array_like (float, 1D)
The input matrix for the PAV algorithm.output : array_like (float, 1D)
The output matrix, must be of the same size as inputReturns:
output : array_like (float, 1D)
The output matrix; will be created in the same size as input
- bob.math.pavxWidth(input, output) → width¶
Applies the Pool-Adjacent-Violators Algorithm and returns the width.
Applies the Pool-Adjacent-Violators Algorithm to input. This is a simplified C++ port of the isotonic regression code made available at the University of Bern website.
Parameters:
input : array_like (float, 1D)
The input matrix for the PAV algorithm.output : array_like (float, 1D)
The output matrix, must be of the same size as inputReturns:
width : array_like (uint64, 1D)
The width matrix will be created in the same size as input
Todo
Explain, what width means in this case
- bob.math.pavxWidthHeight(input, output) → width, height¶
Applies the Pool-Adjacent-Violators Algorithm and returns the width and the height.
Applies the Pool-Adjacent-Violators Algorithm to input. This is a simplified C++ port of the isotonic regression code made available at the University of Bern website.
Parameters:
input : array_like (float, 1D)
The input matrix for the PAV algorithm.output : array_like (float, 1D)
The output matrix, must be of the same size as inputReturns:
width : array_like (uint64, 1D)
The width matrix will be created in the same size as input
Todo
Explain, what width means in this case
height : array_like (float, 1D)
The height matrix will be created in the same size as input
Todo
Explain, what height means in this case
- bob.math.pavx_()¶
- pavx_(input, output) -> None
- pavx_(input) -> output
Applies the Pool-Adjacent-Violators Algorithm
Warning
This variant does not perform any checks on the input matrices and is faster then pavx(). Use it when you are sure your input matrices sizes match.
Applies the Pool-Adjacent-Violators Algorithm to input. This is a simplified C++ port of the isotonic regression code made available at the University of Bern website.
You can use this method in two different formats. The first interface accepts the input and output. The second one accepts the input array input and allocates a new output array, which is returned.
Parameters:
input : array_like (float, 1D)
The input matrix for the PAV algorithm.output : array_like (float, 1D)
The output matrix, must be of the same size as inputReturns:
output : array_like (float, 1D)
The output matrix; will be created in the same size as input
- bob.math.scatter()¶
- scatter(a) -> s, m
- scatter(a, s) -> m
- scatter(a, m) -> s
- scatter(a, s, m) -> None
Computes scatter matrix of a 2D array.
Computes the scatter matrix of a 2D array considering data is organized row-wise (each sample is a row, each feature is a column). The resulting array s is squared with extents equal to the number of columns in a. The resulting array m is a 1D array with the row means of a. This function supports many calling modes, but you should provide, at least, the input data matrix a. All non-provided arguments will be allocated internally and returned.
Parameters:
a : array_like (float, 2D)
The sample matrix, considering data is organized row-wise (each sample is a row, each feature is a column)s : array_like (float, 2D)
The scatter matrix, squared with extents equal to the number of columns in am : array_like (float,1D)
The mean matrix, with with the row means of aReturns:
s : array_like (float, 2D)
The scatter matrix, squared with extents equal to the number of columns in am : array_like (float, 1D)
The mean matrix, with with the row means of a
- bob.math.scatter_(a, s, m) → None¶
Computes scatter matrix of a 2D array.
Warning
This variant does not perform any checks on the input matrices and is faster then scatter().Use it when you are sure your input matrices sizes match.
Computes the scatter matrix of a 2D array considering data is organized row-wise (each sample is a row, each feature is a column). The resulting array s is squared with extents equal to the number of columns in a. The resulting array m is a 1D array with the row means of a. This function supports many calling modes, but you should provide, at least, the input data matrix a. All non-provided arguments will be allocated internally and returned.
Parameters:
a : array_like (float, 2D)
The sample matrix, considering data is organized row-wise (each sample is a row, each feature is a column)s : array_like (float, 2D)
The scatter matrix, squared with extents equal to the number of columns in am : array_like (float,1D)
The mean matrix, with with the row means of a
- bob.math.scatters()¶
- scatters(data) -> sw, sb, m
- scatters(data, sw, sb) -> m
- scatters(data, sw, sb, m) -> None
Computes
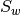 and
and 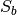 scatter matrices of a set of 2D
arrays.
scatter matrices of a set of 2D
arrays.Computes the within-class
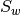 and between-class
and between-class 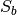 scatter matrices of a set of 2D arrays considering data is organized
row-wise (each sample is a row, each feature is a column), and each
matrix contains data of one class. Computes the scatter matrix of a 2D
array considering data is organized row-wise (each sample is a row,
each feature is a column). The implemented strategy is:
scatter matrices of a set of 2D arrays considering data is organized
row-wise (each sample is a row, each feature is a column), and each
matrix contains data of one class. Computes the scatter matrix of a 2D
array considering data is organized row-wise (each sample is a row,
each feature is a column). The implemented strategy is:- Evaluate the overall mean (m), class means (
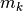 ) and the
) and the total class counts (
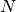 ).
).
- Evaluate the overall mean (m), class means (
Evaluate sw and sb using normal loops.
Note that in this implementation, sw and sb will be normalized by N-1 (number of samples) and K (number of classes). This procedure makes the eigen values scaled by (N-1)/K, effectively increasing their values. The main motivation for this normalization are numerical precision concerns with the increasing number of samples causing a rather large
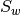 matrix. A normalization strategy mitigates
this problem. The eigen vectors will see no effect on this
normalization as they are normalized in the euclidean sense
(
matrix. A normalization strategy mitigates
this problem. The eigen vectors will see no effect on this
normalization as they are normalized in the euclidean sense
(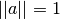 ) so that does not change those.
) so that does not change those.This function supports many calling modes, but you should provide, at least, the input data. All non-provided arguments will be allocated internally and returned.
Parameters:
data : [array_like (float, 2D)]
The list of sample matrices. In each sample matrix the data is organized row-wise (each sample is a row, each feature is a column). Each matrix stores the data of a particular class. Every matrix in ``data`` must have exactly the same number of columns.sw : array_like (float, 2D)
The within-class scatter matrix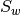 , squared with extents
equal to the number of columns in data
, squared with extents
equal to the number of columns in datasb : array_like (float, 2D)
The between-class scatter matrix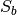 , squared with extents
equal to the number of columns in data
, squared with extents
equal to the number of columns in datam : array_like (float,1D)
The mean matrix, representing the ensemble mean with no prior (i.e., biased towards classes with more samples)Returns:
sw : array_like (float, 2D)
The within-class scatter matrix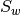
sb : array_like (float, 2D)
The between-class scatter matrix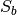
m : array_like (float, 1D)
The mean matrix, representing the ensemble mean with no prior (i.e., biased towards classes with more samples)
- bob.math.scatters_()¶
- scatters_(data, sw, sb, m) -> None
- scatters_(data, sw, sb) -> None
Computes
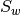 and
and 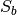 scatter matrices of a set of 2D
arrays.
scatter matrices of a set of 2D
arrays.Warning
This variant does not perform any checks on the input matrices and is faster then scatters(). Use it when you are sure your input matrices sizes match.
For a detailed description of the function, please see scatters().
Parameters:
data : [array_like (float, 2D)]
The list of sample matrices. In each sample matrix the data is organized row-wise (each sample is a row, each feature is a column). Each matrix stores the data of a particular class. Every matrix in ``data`` must have exactly the same number of columns.sw : array_like (float, 2D)
The within-class scatter matrix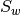 , squared with extents
equal to the number of columns in data
, squared with extents
equal to the number of columns in datasb : array_like (float, 2D)
The between-class scatter matrix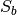 , squared with extents
equal to the number of columns in data
, squared with extents
equal to the number of columns in datam : array_like (float,1D)
The mean matrix, representing the ensemble mean with no prior (i.e., biased towards classes with more samples)